题目内容
对于区间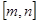 上有意义的两个函数
上有意义的两个函数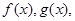 如果有任意
如果有任意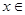
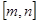 ,均有
,均有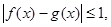 则称
则称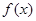 与
与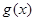 在
在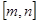 上是接近的,否则称
上是接近的,否则称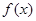 与
与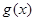 在
在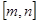 上是非接近的.现有两个函数
上是非接近的.现有两个函数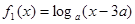 与
与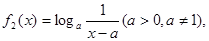 给定区间
给定区间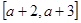 , 讨论
, 讨论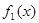 与
与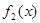 在给定区间
在给定区间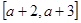 上是否是接近的.
上是否是接近的.
【答案】
当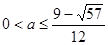 时,
时,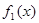 与
与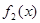 在给定区间
在给定区间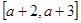 上是接近的.
上是接近的.
【解析】
试题分析: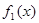 与
与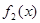 在给定区间
在给定区间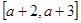 上都有意义,
上都有意义,
则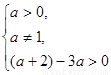 解得
解得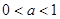
构造函数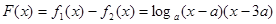 ,
,
函数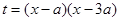 在
在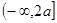 上单调递减,在
上单调递减,在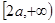 上单调递增,且
上单调递增,且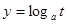 在其定义域内为减函数.
在其定义域内为减函数.
又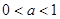 ,得
,得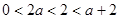 ,故
,故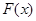 在
在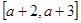 内单调递减.
内单调递减.
只需保证 即
即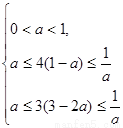
解得当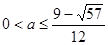 时,
时,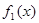 与
与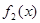 在给定区间
在给定区间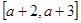 上是接近的.
上是接近的.
考点:本题考查了函数性质的运用
点评:对于函数新定义题,要正确理解题目法则,然后利用函数的相关知识求解即可,属基础题

练习册系列答案
相关题目
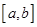 上有意义的两个函数
上有意义的两个函数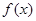 与
与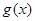 ,如果对任意的
,如果对任意的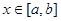 ,均有
,均有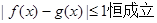 ,则称
,则称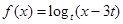 与
与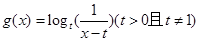 ,给定区间
,给定区间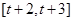 .
.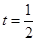 ,求
,求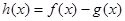 在
在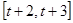 上的值域,判断
上的值域,判断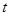 的取值范围;
的取值范围;