Question

8、设α、β是两个不同的平面，a、b是两条不同的直线，给出下列四个命题，其中真命题是（　　）

A、若a∥α，b∥α，则a∥b

B、若a∥α，b∥β，则α∥β

C、若a⊥α，b⊥β，a⊥b，则α⊥β

D、若a、b在平面α内的射影互相垂直，则a⊥b

Answer 1

分析：A选项用空间中直线的位置关系讨论；
B选项用面面平行的条件进行讨论；
C选项用面面垂直的判定定理进行判断；
D选项用线线的位置关系进行讨论，

解答：解：A选项不正确，a∥α，b∥α，两直线的位置关系可能是平行，相交、异面
B选项不正确，两个平面平行于同一条直线，两平面的位置关系可能是平行或者相交．
C选项正确，由b⊥β，a⊥b可得出β∥a或β?a，又a⊥α故有α⊥β
D选项不正确，本命题用图形说明，如图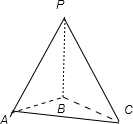三棱锥P-ABC中，侧棱PB垂直于底面，PA，PC两线在底面上的投影垂直，而两线不垂直．
故选C

点评：本题考查平面与平面之间的位置关系，考查了面面垂直的判定面面平行的判定，考查了空间想像能力．