题目内容
已知函数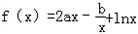 .
.
(I)若f(x)在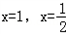 处取极值,
处取极值,
①求a、b的值;
②存在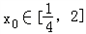 ,使得不等式f(x0)﹣c≤0成立,求c的最小值;
,使得不等式f(x0)﹣c≤0成立,求c的最小值;
(II)当b=a时,若f(x)在(0,+∞)上是单调函数,求a的取值范围.
(参考数据e2≈7.389,e3≈20.08)
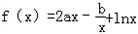 .
.(I)若f(x)在
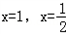 处取极值,
处取极值,①求a、b的值;
②存在
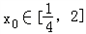 ,使得不等式f(x0)﹣c≤0成立,求c的最小值;
,使得不等式f(x0)﹣c≤0成立,求c的最小值;(II)当b=a时,若f(x)在(0,+∞)上是单调函数,求a的取值范围.
(参考数据e2≈7.389,e3≈20.08)
解:(Ⅰ)①∵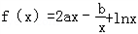 ,定义域为(0,+∞)
,定义域为(0,+∞)
∴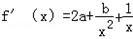
∵f(x)在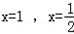 处取得极值,
处取得极值,
∴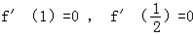
即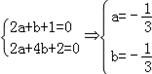 ,
,
所以所求a,b值均为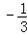
②在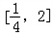 存在x0,使得不等式f(x0)﹣c≤0成立,则只需c≥[f(x)]min
存在x0,使得不等式f(x0)﹣c≤0成立,则只需c≥[f(x)]min
由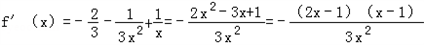
∴当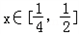 时,f'(x)<0,函数f(x)单调递减;
时,f'(x)<0,函数f(x)单调递减;
当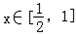 时,f'(x)>0,函数f(x)单调递增;
时,f'(x)>0,函数f(x)单调递增;
当x∈[1,2]时,f'(x)<0,函数f(x)单调递减,
∴f(x)在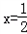 处有极小值
处有极小值
而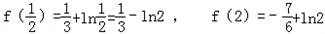
又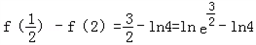 ,
,
因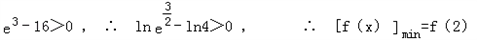 ,
,
∴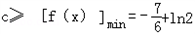 ,
,
∴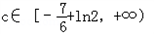 ,
,
故  .
.
(Ⅱ)当 a=b 时,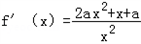
①当a=0时,f(x)=lnx,则f(x)在(0,+∞)上单调递增;
②当a>0时,∵x>0,∴2ax2+x+a>0,
∴f'(x)>0,则f(x)在(0,+∞)上单调递增;
③当a<0时,设g(x)=2ax2+x+a,只需△≤0,
从而得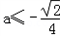 ,此时f(x)在(0,+∞)上单调递减;
,此时f(x)在(0,+∞)上单调递减;
综上可得,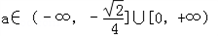

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
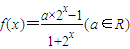 .
.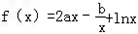 .
. 处取和极值,
处取和极值,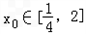 ,使得不等式f(
,使得不等式f(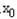 )-c≤0成立,求c的最小值;
)-c≤0成立,求c的最小值;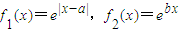 .
.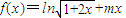 .
.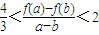 .
.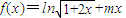 .
.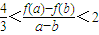 .
.