题目内容
如图,动圆 ,1<t<3,
,1<t<3,
与椭圆 :
: 相交于A,B,C,D四点,点
相交于A,B,C,D四点,点 分别为
分别为 的左,右顶点。
的左,右顶点。
(Ⅰ)当t为何值时,矩形ABCD的面积取得最大值?并求出其最大面积;
(Ⅱ)求直线AA1与直线A2B交点M的轨迹方程。

【答案】
(1)6 (2)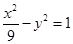
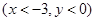
【解析】(1)设 ,则矩形ABCD的面积
,则矩形ABCD的面积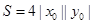 .
.
由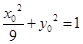 得
得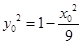 ,从而
,从而
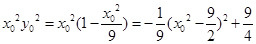
当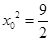 ,
,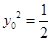 时,
时, .从而
.从而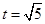 时,矩形ABCD的面积最大,最大面积为6.
时,矩形ABCD的面积最大,最大面积为6.
(2)证明:由  ,
,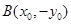 ,
,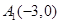 ,
,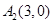 知
知
直线 的方程为
的方程为 ①
①
直线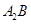 的方程为
的方程为 ②
②
由①②得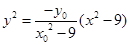 ③
③
又点 在椭圆C上,故
在椭圆C上,故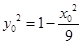 ④
④
将④代入③得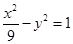
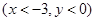
因此点M的轨迹方程为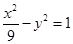
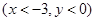 .
.
考点定位:本大题主要考查椭圆、圆、直线的标准方程的求法以及直线与椭圆、圆的位置关系,突出解析几何的基本思想和方法的考查:如数形结合思想、坐标化方法等

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目