题目内容
6.已知函数f(x)=log2(|x+1|+|x-1|-a).(1)当a=4时,求函数f(x)的定义域;
(2)若函数f(x)的定义域是R,求实数a的取值范围.
分析 (1)把a=4代入函数解析式,由真数大于0结合绝对值的几何意义得答案;
(2)把函数f(x)的定义域是R,转化为对于任意实数x,|x+1|+|x-1|-a>0恒成立,分离a后再由绝对值的几何意义得答案.
解答  解:(1)当a=4时,f(x)=log2(|x+1|+|x-1|-4).
解:(1)当a=4时,f(x)=log2(|x+1|+|x-1|-4).
由|x+1|+|x-1|-4>0,结合绝对值的几何意义如图,
可得x<-2或x>2.
∴函数f(x)的定义域为(-∞,-2)∪(2,+∞);
(2)要使函数f(x)的定义域是R,则对于任意实数x,|x+1|+|x-1|-a>0恒成立,
即a<|x+1|+|x-1|恒成立,
由绝对值的几何意义可知,(|x+1|+|x-1|)min=2,
∴a<2.
点评 本题考查函数的定义域及其求法,考查了绝对值的几何意义,考查数学转化思想方法,是中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
16.下列函数中,既是偶数又在区间(0,+∞)上单调递减的是( )
| A. | $y=\frac{1}{x}$ | B. | y=ex | C. | y=-x2 | D. | y=lg|x| |
11.x2+(y+2)2=3的圆心坐标、半径分别为( )
| A. | (0,2);3 | B. | (0,-2);3 | C. | $({0,2});\sqrt{3}$ | D. | $({0,-2});\sqrt{3}$ |
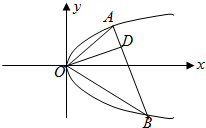 如图,已知直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1).
如图,已知直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1).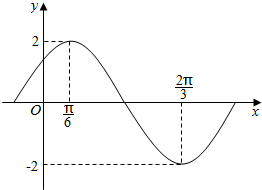 函数$f(x)=Asin(ωx+φ)\;(A>0,ω>0,|φ|<\frac{π}{2})$部分图象如图所示.
函数$f(x)=Asin(ωx+φ)\;(A>0,ω>0,|φ|<\frac{π}{2})$部分图象如图所示.