题目内容
已知关已知关于x的方程2x2-mx-1=0在区间(0,1)上恰有一个实数根,则实数m的取值范围是
- A.(0,1)
- B.(0,+∝)
- C.(1,+∝)
- D.(-∝,1)
D
分析:根据关于x的方程2x2-mx-1=0在区间(0,1)上恰有一个实数根,分类参数,转化为m=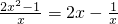 ,在区间(0,1)上恰有一个实数根,即直线y=m与函数y=
,在区间(0,1)上恰有一个实数根,即直线y=m与函数y=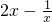 在区间(0,1)上只有一个交点,利用函数的单调性求得该函数的值域,即是实数m的取值范围.
在区间(0,1)上只有一个交点,利用函数的单调性求得该函数的值域,即是实数m的取值范围.
解答:∵2x2-mx-1=0,
∴m=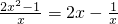 ,
,
由于函数y=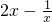 在区间(0,1)上是增函数且值域为(-∞,1),
在区间(0,1)上是增函数且值域为(-∞,1),
故选D
点评:此题考查了方程的根与函数图象交点之间的关系,体现了转化的思想,利用函数的单调性求函数y=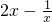 在区间(0,1)上的值域是解决此题的关键,属中档题.
在区间(0,1)上的值域是解决此题的关键,属中档题.
分析:根据关于x的方程2x2-mx-1=0在区间(0,1)上恰有一个实数根,分类参数,转化为m=
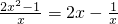 ,在区间(0,1)上恰有一个实数根,即直线y=m与函数y=
,在区间(0,1)上恰有一个实数根,即直线y=m与函数y=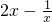 在区间(0,1)上只有一个交点,利用函数的单调性求得该函数的值域,即是实数m的取值范围.
在区间(0,1)上只有一个交点,利用函数的单调性求得该函数的值域,即是实数m的取值范围.解答:∵2x2-mx-1=0,
∴m=
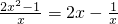 ,
,由于函数y=
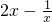 在区间(0,1)上是增函数且值域为(-∞,1),
在区间(0,1)上是增函数且值域为(-∞,1),故选D
点评:此题考查了方程的根与函数图象交点之间的关系,体现了转化的思想,利用函数的单调性求函数y=
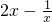 在区间(0,1)上的值域是解决此题的关键,属中档题.
在区间(0,1)上的值域是解决此题的关键,属中档题. 
练习册系列答案
相关题目