题目内容
方程10x+x-2=0解的个数为
1
1
．分析：构造两个函数y=10x和y=2-x分别画出图象，利用有无交点来判断根的个数．
解答：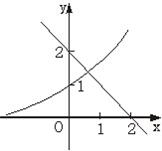
解：方程的解可看作函数y=2x和y=2-x的图象交点的横坐标，
分别画函数y=10x与y=2-x的图象，如图，只有一个交点，故方程只有一解．
故答案为：1．
解：方程的解可看作函数y=2x和y=2-x的图象交点的横坐标，分别画函数y=10x与y=2-x的图象，如图，只有一个交点，故方程只有一解．
故答案为：1．
点评：此题考查根的存在性及根的个数，无法直接求解的方程问题，常用作图法来解，注意数形结合的思想．
练习册系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目