题目内容
设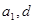 为实数,首项为
为实数,首项为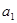 ,公差为
,公差为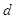 的等差数列
的等差数列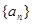 的前n项和为
的前n项和为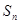 ,满足
,满足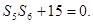
(1)若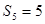 ,求
,求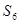 及
及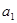 ;
;
(2)求d的取值范围.
【解析】本试题主要考查了数列的求和的运用以及通项公式的运用。第一问中,利用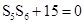 和已知的
和已知的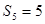 ,得到结论
,得到结论
第二问中,利用首项和公差表示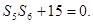 ,则方程是一个有解的方程,因此判别式大于等于零,因此得到d的范围。
,则方程是一个有解的方程,因此判别式大于等于零,因此得到d的范围。
解:(1)因为设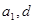 为实数,首项为
为实数,首项为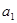 ,公差为
,公差为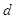 的等差数列
的等差数列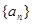 的前n项和为
的前n项和为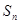 ,满足
,满足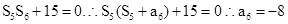
所以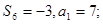
(2)因为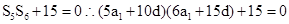
得到关于首项的一个二次方程,则方程必定有解,结合判别式求解得到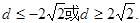
【答案】
(1) 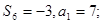 (2)
(2)
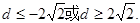

练习册系列答案
相关题目