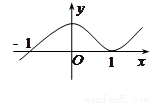题目内容
已知函数的图象如图所示，则其函数解析式可能是（ ）
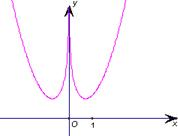
| A、f（x）=x2+ln|x| | B、f（x）=x2-ln|x| | C、f（x）=x+ln|x| | D、f（x）=x-ln|x| |
分析：本题是选择题，可采用排除法，根据函数的对称性可排除选项C和选项D，再根据函数在（0，1）上的单调性排除选项A，即可得到所求．
解答：解：根据函数图象关于y轴对称可知函数为偶函数，故可排除选项C和选项D
根据函数图象可知函数在（0，1）上单调递减．
选项A、f（x）=x2+ln|x|=x2+lnx
f'（x）=2x+
＞0在（0，1）上恒成立．
∴函数在（0，1）上单调递增故不正确．
故选B
根据函数图象可知函数在（0，1）上单调递减．
选项A、f（x）=x2+ln|x|=x2+lnx
f'（x）=2x+
| 1 |
| x |
∴函数在（0，1）上单调递增故不正确．
故选B
点评：本题主要考查了识图能力，以及函数的对称性和单调性，数形结合的思想，属于基础题．
练习册系列答案
相关题目
的图象如图所示，
，则
．
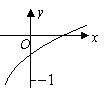已知函数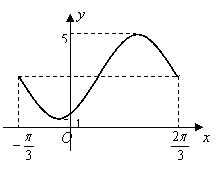
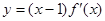的图象如图所示，则
满足的关系是（ ）
B．
D．
的图象如图所示．
的解析式；
，且方程
有两个不同的实数根，求实数
的取值范围和这两个根的和；
中，若
，求
的取值范围．
的图象如图所示，其中
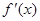为函数
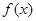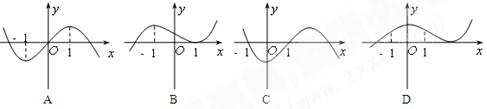
的导函数，则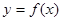
的大致图象是( )
