题目内容
若随机变量ξ服从几何分布,且p(ξ=k)=g(k,p)(0<p<1),试写出随机变量ξ的期望公式,并给出证明.
证明:如下表
ξ 1 2 3 4 …k …
P p qp q2p q3p …qk-1p …
则Eξ=p+2qp+3q2p+…+kqk-1p+…
=p(1+2q+3q2+…+kqk-1+…)
令T=1+2q+3q2+4q3 …+kqk-1+(k+1)qk +…①
则qT=q+2q2+3q3+…+(k-1)qk-1+kqk+…②
①-②T-qT=q0+q1+q2+q3+…+qk-1+qk +…
=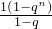
即T=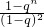 =
=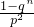 (n→∞)
(n→∞)
则Eξ=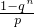 (n→∞)
(n→∞)
∴当n→∞时,Eξ=
分析:根据变量符合几何分布,写出各个变量对应的概率,表示出期望的表达式,利用数列中的错位相减得到数列的前n项和,根据n是一个趋近于无穷的数字,利用极限的思想得到结果.
点评:本题看出几何分布的期望值的推导,本题解题的关键是利用数列的求和的方法来写出期望的表示式,本题是一个中档题目.
ξ 1 2 3 4 …k …
P p qp q2p q3p …qk-1p …
则Eξ=p+2qp+3q2p+…+kqk-1p+…
=p(1+2q+3q2+…+kqk-1+…)
令T=1+2q+3q2+4q3 …+kqk-1+(k+1)qk +…①
则qT=q+2q2+3q3+…+(k-1)qk-1+kqk+…②
①-②T-qT=q0+q1+q2+q3+…+qk-1+qk +…
=
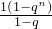
即T=
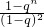 =
=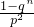 (n→∞)
(n→∞)则Eξ=
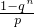 (n→∞)
(n→∞)∴当n→∞时,Eξ=

分析:根据变量符合几何分布,写出各个变量对应的概率,表示出期望的表达式,利用数列中的错位相减得到数列的前n项和,根据n是一个趋近于无穷的数字,利用极限的思想得到结果.
点评:本题看出几何分布的期望值的推导,本题解题的关键是利用数列的求和的方法来写出期望的表示式,本题是一个中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目