题目内容
已知A、B、C为直线l上三点，且AB=BC=a；P为l外一点，且∠APB=90°，∠BPC=45°，求（1）∠PBA的正弦、余弦、正切；
（2）PB的长；
（3）P点到l的距离．
分析：（1）过P点作PD⊥AB交AB于点D，过点B作BE∥AP交PC于点E依题意可知∠PBE=90°，∠PEB=45°，PB=BE，再根据△CPA∽△CEB相应边的比相等，可求的
，由于PB=BE，进而可得
的值，求得tan∠PBA，再根据同角三角函数关系可求得cos∠PBA和sin∠PBA．
（2）在直角三角形APB中，根据PB=AB•cos∠PBA求得PB．
（3）P点到l的距离即为图中PD的长度，在直角三角形PDB中，根据PD=PB•sin∠PBA，求得PD的长度．
| PA |
| BE |
| PA |
| PB |
（2）在直角三角形APB中，根据PB=AB•cos∠PBA求得PB．
（3）P点到l的距离即为图中PD的长度，在直角三角形PDB中，根据PD=PB•sin∠PBA，求得PD的长度．
解答：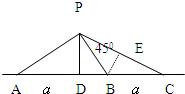
解：过P点作PD⊥AB交AB于点D（如图）
（1）过点B作BE∥AP交PC于点E
则∠PBE=90°，∠PEB=45°，PB=BE．
∵△CPA∽△CEB，
∴
=
=2，
因PB=BE，
∴
=2，tan∠PBA=2．
又∵1+tg2∠PBA=sec2∠PBA，∠PBA为锐角，
∴sec∠PBA=
=
，cos∠PBA=
=
，sin∠PBA=tan∠PBA•cos∠PBA=
．
（2）PB=AB•cos∠PBA=
a．
（3）∵PB=
a，sin∠PBA=
，
∴PD=PB•sin∠PBA=
a．
综上，所求为
（1）∠PBA的正弦、余弦、正切分别是
，
，2；
（2）PB的长为
a；
（3）P点到l的距离为
a．
解：过P点作PD⊥AB交AB于点D（如图）（1）过点B作BE∥AP交PC于点E
则∠PBE=90°，∠PEB=45°，PB=BE．
∵△CPA∽△CEB，
∴
| PA |
| BE |
| 2a |
| a |
因PB=BE，
∴
| PA |
| PB |
又∵1+tg2∠PBA=sec2∠PBA，∠PBA为锐角，
∴sec∠PBA=
| 1+tg2∠PBA |
| 5 |
| 1 | ||
|
| ||
| 5 |
2
| ||
| 5 |
（2）PB=AB•cos∠PBA=
| ||
| 5 |
（3）∵PB=
| ||
| 5 |
2
| ||
| 5 |
∴PD=PB•sin∠PBA=
| 2 |
| 5 |
综上，所求为
（1）∠PBA的正弦、余弦、正切分别是
| 2 |
| 5 |
| 5 |
| 1 |
| 5 |
| 5 |
（2）PB的长为
| 1 |
| 5 |
| 5 |
（3）P点到l的距离为
| 2 |
| 5 |
点评：本题主要考查三角形中的几何计算．要充分利用好三角形中的特殊角如90°，60°，45°等利用三角函数关系来解决问题．
练习册系列答案
口算题天天练系列答案
相关题目