题目内容
若Sn和Tn分别表示数列{an}和{bn}的前n项和,对任意自然数n,有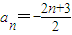 ,4Tn-12Sn=13n.
,4Tn-12Sn=13n.(1)求数列{bn}的通项公式;
(2)设集合A={x|x=2an,n∈N*},B={y|y=4bn,n∈N*}.若等差数列{cn}任一项cn∈A∩B,c1是A∩B中的最大数,且-265<c10<-125,求{cn}的通项公式.
【答案】分析:(1)由4Tn-12Sn=13n可得4Tn-1-12Sn-1=13(n-1),两式相减,结合an可求bn
(2)由题意可得,A∩B=B,由c1是A∩B中的最大数可得c1=-17,d=-12k,由-265<c10<-125可得,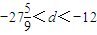 ,从而可得等差数列{cn}的公差d,代入求解即可
,从而可得等差数列{cn}的公差d,代入求解即可
解答:解:(1)当n≥2,n∈N*时: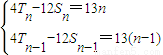 ,
,
两式相减得:4bn-12an=13,∴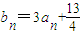 =
=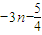 ,
,
又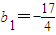 也适合上式,
也适合上式,
∴数列{bn}的通项公式为bn=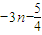 .
.
(2)对任意n∈N*,2an=-2n-3,
4bn=-12n-5=-2(6n+1)-3,∴B?A,∴A∩B=B
∵c1是A∩B中的最大数,∴c1=-17,
设等差数列{cn}的公差为d,则c10=-17+9d,
∴-265<-17+9d<-125,即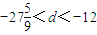 ,
,
又4bn是一个以-12为公差的等差数列,
∴d=-12k(k∈N*),∴d=-24,∴cn=7-24n.
点评:本题主要考查了数列递推公式的应用,利用构造法求数列的通项公式,解决本题还要求考生具备一定的推理的能力.
(2)由题意可得,A∩B=B,由c1是A∩B中的最大数可得c1=-17,d=-12k,由-265<c10<-125可得,
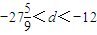 ,从而可得等差数列{cn}的公差d,代入求解即可
,从而可得等差数列{cn}的公差d,代入求解即可解答:解:(1)当n≥2,n∈N*时:
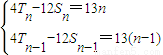 ,
,两式相减得:4bn-12an=13,∴
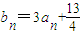 =
=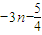 ,
,又
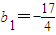 也适合上式,
也适合上式,∴数列{bn}的通项公式为bn=
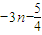 .
.(2)对任意n∈N*,2an=-2n-3,
4bn=-12n-5=-2(6n+1)-3,∴B?A,∴A∩B=B
∵c1是A∩B中的最大数,∴c1=-17,
设等差数列{cn}的公差为d,则c10=-17+9d,
∴-265<-17+9d<-125,即
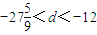 ,
,又4bn是一个以-12为公差的等差数列,
∴d=-12k(k∈N*),∴d=-24,∴cn=7-24n.
点评:本题主要考查了数列递推公式的应用,利用构造法求数列的通项公式,解决本题还要求考生具备一定的推理的能力.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
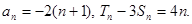
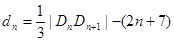 ,求dn;
,求dn;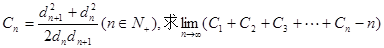 的值.
的值.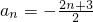 ,4Tn-12Sn=13n.
,4Tn-12Sn=13n.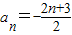 ,4Tn-12Sn=13n.
,4Tn-12Sn=13n.