题目内容
设一元二次不等式ax2+bx+1>0的解集为{x|-1<x<2},则a+b的值是( )
分析:根据一元二次不等式ax2+bx+1>0的解集为{x|-1<x<2},可得方程ax2+bx+1=0的解为-1,2,利用韦达定理即可解答本题.
解答:解:∵一元二次不等式ax2+bx+1>0的解集为{x|-1<x<2},
∴方程ax2+bx+1=0的解为-1,2
∴-1+2=-
,(-1)×2=
∴a=-
,b=
∴a+b=0
故选C.
∴方程ax2+bx+1=0的解为-1,2
∴-1+2=-
| b |
| a |
| 1 |
| a |
∴a=-
| 1 |
| 2 |
| 1 |
| 2 |
∴a+b=0
故选C.
点评:本题重点考查一元二次不等式的解集,明确一元二次不等式的解集与方程解之间的关系是解题的关键,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
设一元二次不等式ax2+bx+1>0的解集为{x|-1<x<3},则a?b的值为( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
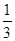 },则ab的值是( )
},则ab的值是( )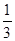 },则ab的值是
_____.
},则ab的值是
_____.