题目内容
18.设P为曲线C:y=$\sqrt{x}$和直线y=m(m>0)的交点,l1是曲线C在P点处的切线.(1)求直线y=m关于l1的对称直线l2的方程;
(2)判断直线l2是否通过一个与m无关的定点,若通过,求此定点的坐标;若不通过,请说明理由.
分析 (1)求得P的坐标,求出y=$\sqrt{x}$的导数,求得切线的斜率,以及切线方程,在直线y=m上取一点(0,m),关于直线l1的对称点为(a,b),运用中点坐标公式和两直线垂直的条件,解方程可得a,b,进而得到直线l2的方程;
(2)由直线l2的方程,可令x=$\frac{1}{4}$,可得y=0,即可判断直线l2通过一个与m无关的定点.
解答 解:(1)P为曲线C:y=$\sqrt{x}$和直线y=m(m>0)的交点,
即有P(m2,m),
y=$\sqrt{x}$的导数为y′=$\frac{1}{2}$•$\frac{1}{\sqrt{x}}$,
曲线C在P点处的切线斜率为k=$\frac{1}{2m}$,
即有曲线C在P点处的切线方程为l1:y-m=$\frac{1}{2m}$(x-m2),
即为x-2my+m2=0,
在直线y=m上取一点(0,m),关于直线l1的对称点为(a,b),
即有$\frac{b-m}{a}$=-2m,$\frac{a}{2}$-m(m+b)+m2=0,
解得a=$\frac{2{m}^{2}}{1+4{m}^{2}}$,b=$\frac{m}{1+4{m}^{2}}$.
即有l2的斜率为$\frac{\frac{m}{1+4{m}^{2}}-m}{\frac{2{m}^{2}}{1+4{m}^{2}}-{m}^{2}}$=$\frac{4m}{4{m}^{2}-1}$,
则l2:y-m=$\frac{4m}{4{m}^{2}-1}$(x-m2),
即有对称直线l2的方程为y=$\frac{4m}{4{m}^{2}-1}$x-$\frac{m}{4{m}^{2}-1}$;
(2)由直线l2的方程为y=$\frac{4m}{4{m}^{2}-1}$x-$\frac{m}{4{m}^{2}-1}$;
可令x=$\frac{1}{4}$,可得y=$\frac{4m}{4{m}^{2}-1}$•$\frac{1}{4}$-$\frac{m}{4{m}^{2}-1}$=0,
故直线l2通过一个与m无关的定点,此定点的坐标为($\frac{1}{4}$,0).
点评 本题考查导数的运用:求切线的方程,主要考查导数的几何意义和直线和直线的对称问题,同时考查直线恒过定点问题,属于中档题和易错题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
 矩形ABCD所在平面垂直于三角形ABE所在平面,AB=2AE=3,AD=2,∠ABE=30°,点F为线段BE靠近点E的一个三等分点,点P在线段CD上移动.
矩形ABCD所在平面垂直于三角形ABE所在平面,AB=2AE=3,AD=2,∠ABE=30°,点F为线段BE靠近点E的一个三等分点,点P在线段CD上移动. 在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.
在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.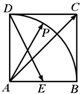 在正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧上的任意一点,设向量$\overrightarrow{AC}=λ\overrightarrow{DE}+μ\overrightarrow{AP}$,当∠PAB=$\frac{π}{3}$时,λ+μ=2,当∠PAB∈[0,$\frac{π}{2}$]时,λ+μ的最小值为$\frac{1}{2}$.
在正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧上的任意一点,设向量$\overrightarrow{AC}=λ\overrightarrow{DE}+μ\overrightarrow{AP}$,当∠PAB=$\frac{π}{3}$时,λ+μ=2,当∠PAB∈[0,$\frac{π}{2}$]时,λ+μ的最小值为$\frac{1}{2}$.