题目内容
对于常数列1,1,1,…,在第1项与第2项之间插入一个数2,在第2项与第3项之间插入两个数2,在第3项与第4项之间插入三个数2,依次类推,即在第n项与第n+1项之间插入n个数2,得到一个新数列![]() :1,2,1,2,2,1,2,2,2,1,2,2,2,2,1,2,…,则数列
:1,2,1,2,2,1,2,2,2,1,2,2,2,2,1,2,…,则数列![]() 的前1234项的和等于( )
的前1234项的和等于( )
A.2450 B.2419 C.2468 D.4919
B
解析:
将数列![]() 作如下分组:
作如下分组:
第1组:1,2;第2组:1,2,2;第3组:1,2,2,2;……;第n组:![]() 。
。
则前n组共有![]() 项。
项。
当n=48时,有![]() 项,n=49时,有
项,n=49时,有![]() 项。
项。
所以前1234项可以排满前48组,在第49组只能排前10项。因此,数列![]() 的前1234项中有49个1,其余的数都是2。
的前1234项中有49个1,其余的数都是2。
故数列![]() 的前1234项的和S=49+(1234-49)
的前1234项的和S=49+(1234-49)![]() 2=2419,故选B。
2=2419,故选B。

练习册系列答案
相关题目
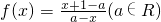 ,
,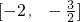 ;
;