题目内容
(14分)某公司计划2008年在甲,乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲,乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问:该公司如何分配在甲乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
【答案】
该公司分配在甲乙两个电视台的广告时间分别为100分钟和200分钟时,公司收益最大,最大收益为70万元.
【解析】
试题分析:设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟,
总收益为z元,由题意得
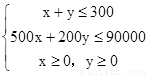 ,
,
目标函数为z=3000x+2000y.
二元一次不等式组等价于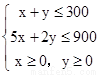
作出二元一次不等式组所表示的平面区域,即可行域.
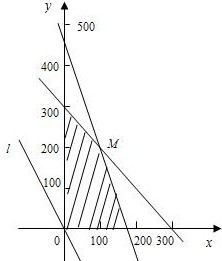
如图,作直线l:3000x+2000y=0,即3x+2y=0.
平移直线l,从图中可知,当直线l过M点时,目标函数取得最大值.
联立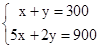
解得x=100,y=200.
∴点M的坐标为(100,200).
∴zmax=3000x+2000y=700000(元)
答:该公司分配在甲乙两个电视台的广告时间分别为100分钟和200分钟时,公司收益最大,最大收益为70万元.
考点:本题主要考查简单线性规划的应用。
点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解。

练习册系列答案
相关题目
 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?