题目内容
将函数f(x)=ax图象向右平移n个单位得函数g(x)的图象,由f(x),g(x)的图象及直线y=1和y=3围成的封闭图形的面积为6,则n=( )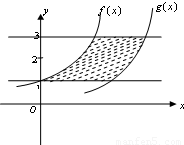
A.1
B.2
C.3
D.4
【答案】分析:由题意及所给的图象可以看出,此题可用割补法将不规则图形变为规则图形,从而达到求出n的值的目的,可作出如图的图形(见解答),由图及题设条件易得n的值
解答: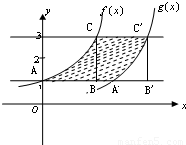 解:如右图,可作出如图的曲边三角形ABC与曲边三角形A′B′C′,其中角B与角B′都是直角
解:如右图,可作出如图的曲边三角形ABC与曲边三角形A′B′C′,其中角B与角B′都是直角
由题意函数f(x)=ax图象向右平移n个单位得函数g(x)的图象,
得两曲边三角形面积相等,由此知,阴影部分的面积即是矩形BCB′C′的面积,
又f(x),g(x)的图象及直线y=1和y=3围成的封闭图形的面积为6,
∴矩形BCB′C′的边BC=2,矩形的面积为6
∴CC′=3,
即函数f(x)=ax图象向右平移3个单位得函数g(x)的图象
∴n=3
故选C
点评:本题的考点是函数的图象与图象的变化,考查了识图的能力及根据图象的特征变换求面积的能力,解题的关键是理解图形,对图形进行割补将其变为规则图形--矩形,从而为利用面积公式求值带来可能
解答:
 解:如右图,可作出如图的曲边三角形ABC与曲边三角形A′B′C′,其中角B与角B′都是直角
解:如右图,可作出如图的曲边三角形ABC与曲边三角形A′B′C′,其中角B与角B′都是直角由题意函数f(x)=ax图象向右平移n个单位得函数g(x)的图象,
得两曲边三角形面积相等,由此知,阴影部分的面积即是矩形BCB′C′的面积,
又f(x),g(x)的图象及直线y=1和y=3围成的封闭图形的面积为6,
∴矩形BCB′C′的边BC=2,矩形的面积为6
∴CC′=3,
即函数f(x)=ax图象向右平移3个单位得函数g(x)的图象
∴n=3
故选C
点评:本题的考点是函数的图象与图象的变化,考查了识图的能力及根据图象的特征变换求面积的能力,解题的关键是理解图形,对图形进行割补将其变为规则图形--矩形,从而为利用面积公式求值带来可能

练习册系列答案
相关题目
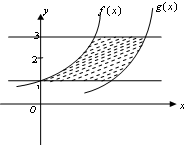 将函数f(x)=ax图象向右平移n个单位得函数g(x)的图象,由f(x),g(x)的图象及直线y=1和y=3围成的封闭图形的面积为6,则n=( )
将函数f(x)=ax图象向右平移n个单位得函数g(x)的图象,由f(x),g(x)的图象及直线y=1和y=3围成的封闭图形的面积为6,则n=( )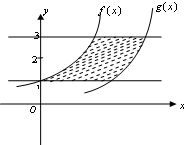 将函数f(x)=ax图象向右平移n个单位得函数g(x)的图象,由f(x),g(x)的图象及直线y=1和y=3围成的封闭图形的面积为6,则n=
将函数f(x)=ax图象向右平移n个单位得函数g(x)的图象,由f(x),g(x)的图象及直线y=1和y=3围成的封闭图形的面积为6,则n=