题目内容
在数列 中,
中, ,
, ,其中
,其中 .
.
(1)设 ,求数列
,求数列 的通项公式;
的通项公式;
(2)记数列 的前
的前 项和为
项和为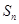 ,试比较
,试比较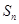 与
与 的大小.
的大小.
【答案】
(1)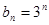 .(2)所以,当
.(2)所以,当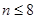 时,
时,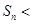
 ;所以,当
;所以,当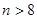 时,
时,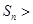
 .
.
【解析】(1) 由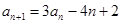 得
得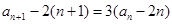 ,
,
又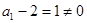 ,
,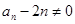 ,得
,得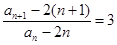 ,从而证明数列
,从而证明数列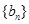 为等比数列,因而易求其通项公式.
为等比数列,因而易求其通项公式.
(2)在(1)的条件下,可求出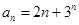 ,从而可利用分组求和的方式得到
,从而可利用分组求和的方式得到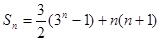 ,进而得到
,进而得到 ,再令
,再令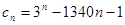 ,
,
利用作差比较的方法研究数列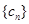 的单调性即可确定
的单调性即可确定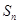 与
与 的大小关系.
的大小关系.
(1)由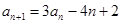 得
得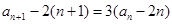 ,
,
又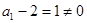 ,
,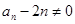 ,得
,得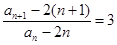 ,
,
所以,数列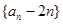 是首项为3,公比为3的等比数列,
是首项为3,公比为3的等比数列,
所以,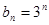 .
.
(2)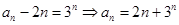 ,
,
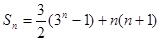 ,
,
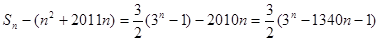 .
.
设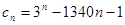 ,
,
由于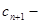
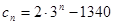
当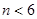 时,
时,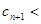
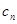
当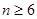 时,
时,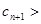
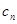
即,当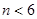 时,数列
时,数列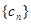 是递减数列,当
是递减数列,当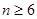 时,数列
时,数列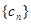 是递增数列
是递增数列
又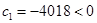 ,
,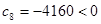 ,
,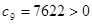
所以,当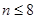 时,
时,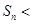
 ;
;
所以,当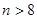 时,
时,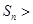
 .
.

练习册系列答案
相关题目
 中,如果存在非零常数
中,如果存在非零常数 ,使得
,使得 对于任意非零正整数
对于任意非零正整数 均成立,那么就称数列
均成立,那么就称数列 满足
满足 (
( )且
)且 ,
,
 ,当
,当 中,若
中,若 ,(
,(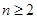 ,
,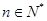 ,
,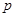 为常数),则称
为常数),则称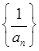 是等差数列;
是等差数列; 是“等方差数列”;
是“等方差数列”;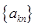 (
( ,
, 为常数)也是“等方差数列”;
为常数)也是“等方差数列”;