题目内容
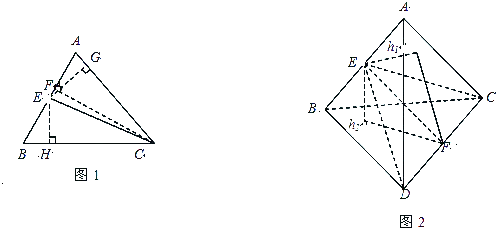
在△ABC（如图1），若CE是∠ACB的平分线，则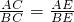
．其证明过程如下：
作EG⊥AC于点G，EH⊥BC于点H，CF⊥AB于点F，
∵CE是∠ACB的平分线，
∴EG=EH．
又∵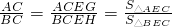
，
，
∴
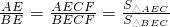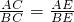
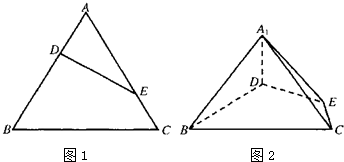
（1）把上面结论推广到空间中：在四面体A-BCD中（如图2），平面CDE是二面角A-CD-B的角平分面，类比三角形中的结论，你得到的相应空间的结论是________
（2）证明你所得到的结论．
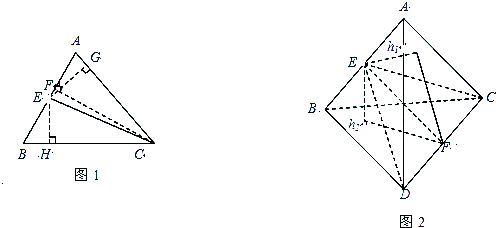
解：在平面中在△ABC（如图1），若CE是∠ACB的平分线，则．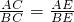
将这个结论类比到空间：在四面体A-BCD中（如图2），平面CDE是二面角A-CD-B的角平分面，
则类比的结论为根据面积类比体积，长度类比面积可得：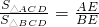
，
证明：设点E到平面ACD、平面BCD的距离分别为h1、h2，则由平面CDE是二面角A-CD-B的角平分面，知h1=h2，
又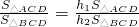
=
，
∴．
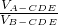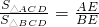故答案为：．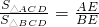
分析：三角形的内角平分线定理类比到空间三棱锥，根据长度类比面积，从而得到．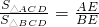
点评：本题考查了类比推理，将平面中的性质类比到空间．属于基础题．
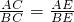．将这个结论类比到空间：在四面体A-BCD中（如图2），平面CDE是二面角A-CD-B的角平分面，
则类比的结论为根据面积类比体积，长度类比面积可得：
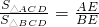，证明：设点E到平面ACD、平面BCD的距离分别为h1、h2，则由平面CDE是二面角A-CD-B的角平分面，知h1=h2，
又
=，∴
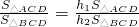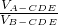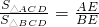．故答案为：
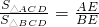．分析：三角形的内角平分线定理类比到空间三棱锥，根据长度类比面积，从而得到
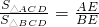．点评：本题考查了类比推理，将平面中的性质类比到空间．属于基础题．
练习册系列答案
相关题目
如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6．D、E分别是AC、AB上的点，且DE∥BC，将△ADE沿DE折起到△A1DE的位置，使A1D⊥CD，如图2．
