题目内容
(本题满分12分)在△ABC中,三内角A、B、C成等差数列,角B的对边b为1,求证:1<a+c≤2.
略
证法一:∵2B=A+C,又A+B+C=180°,
∴B=60°,C=120°-A.
由正弦定理得
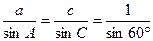 ,
,再由合分比定理得a+c=
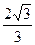 (sinA+sinC)=
(sinA+sinC)=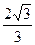 [sinA+sin(120°-A)]=2sin(A+30°)≤2,
[sinA+sin(120°-A)]=2sin(A+30°)≤2,再由两边之和大于第三边,∴1<a+c.
∴1<a+c≤2.
证法二:先得B=60°(同上得).
再利用余弦定理知cosB=
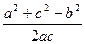 ,即
,即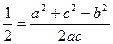 ,
,即(a+c)2-1=3ac≤
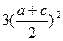 .
.解得a+c≤2.
又∵a+c>1,∴1<a+c≤2.

练习册系列答案
相关题目
 , b=
, b= , B=60°那么角A等于 ( )
, B=60°那么角A等于 ( )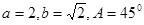 ,则B等于
,则B等于 分别为角A、B、C的对边,
分别为角A、B、C的对边, ,
, ="3," △ABC的面积为6
="3," △ABC的面积为6 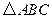 中,角
中,角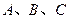 所对的边分别为
所对的边分别为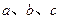 ,已知
,已知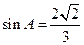 ,(Ⅰ)求
,(Ⅰ)求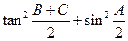 的值;(Ⅱ)若
的值;(Ⅱ)若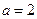 ,
,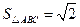 ,求
,求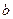 的值.
的值.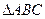 中,A.B.C的对边分别为
中,A.B.C的对边分别为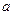 ,
,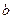 ,
,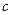 。且
。且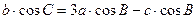 ,
,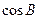 的值
的值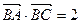 ,
,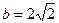 ,求
,求 且
且 成等差数列。则
成等差数列。则 的范围是
的范围是 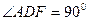 ,G是DF上一动点
,G是DF上一动点 GN垂直AC
GN垂直AC

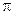 )与x轴围成的图形的面积为
)与x轴围成的图形的面积为