题目内容
已知双曲线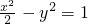
，过点P（0，1）作斜率为k的直线l与双曲线恰有一个公共点，求满足条件的直线l．
解：（1）依题意设直线方程为y=kx+1，由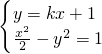
得（1-2k2）x2-4kx-4=0…（3分）
当1-2k2=0，即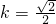
时，方程只一个实根，直线为
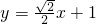…（3分）
当1-2k2≠0，即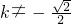
时，由△=0得k=±1，直线为y=±x+1…（3分）
故所求方程为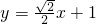或y=±x+1…（1分）
分析：先假设直线方程为y=kx+1，与双曲线方程联立消去y得（1-2k2）x2-4kx-4=0，由于直线l与双曲线恰有一个公共点，而方程不一定是二次方程，故需分类讨论．
点评：本题主要考查直线与双曲线的位置关系，通过建立方程组消元，应注意分类讨论．
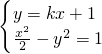得（1-2k2）x2-4kx-4=0…（3分）当1-2k2=0，即
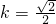时，方程只一个实根，直线为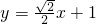…（3分）当1-2k2≠0，即
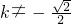时，由△=0得k=±1，直线为y=±x+1…（3分）故所求方程为
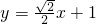或y=±x+1…（1分）分析：先假设直线方程为y=kx+1，与双曲线方程联立消去y得（1-2k2）x2-4kx-4=0，由于直线l与双曲线恰有一个公共点，而方程不一定是二次方程，故需分类讨论．
点评：本题主要考查直线与双曲线的位置关系，通过建立方程组消元，应注意分类讨论．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
，过点P（1，1）能否作一条直线l，与双曲线交于A，B两点，且点P是线段AB的中点？如果能，求出直线l的方程；如果不能，请说明理由．
，过点P（1，1）能否作一条直线l，与双曲线交于A，B两点，且点P是线段AB的中点？如果能，求出直线l的方程；如果不能，请说明理由．
，过点P（1，1）能否作一条直线l，与双曲线交于A，B两点，且点P是线段AB的中点？如果能，求出直线l的方程；如果不能，请说明理由．