题目内容
5.设奇函数f(x)满足f(x)=$\left\{\begin{array}{l}{-1(x≥1)}\\{1(0<x<1)}\end{array}\right.$,则f[f(sin6)]=( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 求出f(-sin6)=1,利用函数f(x)是奇函数,可得f(sin6)]=-1,即可得出结论.
解答 解:∵-1<sin6<0,
∴0<-sin6<1,
∴f(-sin6)=1,
∵函数f(x)是奇函数,
∴f(sin6)]=-1,
∴f[f(sin6)]=f(-1)=-f(1)=1,
故选:C.
点评 本题考查函数值的计算,考查函数的奇偶性,考查学生的计算能力,比较基础.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
10. 如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )
如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )
 如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )
如图四边形ABCD,AB=BD=DA=2.BC=CD=$\sqrt{2}$,现将△ABD沿BD折起,使二面角A-BD-C的大小在[$\frac{π}{6}$,$\frac{5π}{6}$],则直线AB与CD所成角的余弦值取值范围是( )| A. | [0,$\frac{\sqrt{2}}{8}$]∪($\frac{5\sqrt{2}}{8}$,1) | B. | [$\frac{\sqrt{2}}{8}$,$\frac{5\sqrt{2}}{8}$] | C. | [0,$\frac{\sqrt{2}}{8}$] | D. | [0,$\frac{5\sqrt{2}}{8}$] |
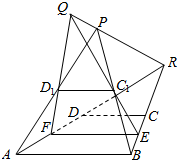 梯形ABCD沿中位线EF折起成空间图形ABEC1D1F,求证:
梯形ABCD沿中位线EF折起成空间图形ABEC1D1F,求证: