��Ŀ����
������{xn}��������Dz�����1������,ǰn���ΪSn,��֪��Pn(xn,Sn)��ֱ��y=kx+b��(����,����k��0,��k��1),��yn=log0.5xn.(1)��֤:����{xn}�ǵȱ�����;
(2)���yn=18-3n,��ʵ��k,b��ֵ;
(3)�������t,s��N*,s��t��ʹ�õ㣨t,ys���ͣ�s,yt������ֱ��y=2x+1��,���ж�,�Ƿ������Ȼ��M,��n��Mʱ,xn��1�����?������,���M����Сֵ,��������,��˵������.
��:(1)֤�����ߵ�Pn,Pn+1����ֱ��y=kx+b��,��![]() =k,��(k-1)xn+1=kxn.
=k,��(k-1)xn+1=kxn.
�߳���k��0,��k��1,��![]() (���㳣��).������{xn}�ǵȱ�����.
(���㳣��).������{xn}�ǵȱ�����.
(2)��yn=log0.5xn,��xn=![]() =8n-6=8-58n-1,��
=8n-6=8-58n-1,��![]() =8,��k=
=8,��k=![]() .
.
��Pn��ֱ����,��Sn=kxn+b,��n=1��b=S1![]() x1=
x1=![]() x1=
x1=![]() .
.
(3)xn��1������ȼ���yn��0,
�ߴ���t,s��N��ʹ��(t,ys)�ͣ�s,yt)����y=2x+1��,��ys=2t+1,��
yt=2s+1,��
��-��,��ys-yt=2(t-s).��֤{yn}�ǵȲ�����,���乫��Ϊd,����ys-yt=(s-t)d,
��s��t,��d=-2��0.��+��,��ys+yt=2(t+s)+2,
��ys+yt=y1+(s-1)(-2)+y1+(t-1)(-2)=2y1-2(s+t)+4,
��2y1-2(s+t)+4=2(t+s)+2,��y1=2(t+s)-1��0,
������{yn}������Ϊ��,����Ϊ���ĵȲ�����,
��һ������һ����С��Ȼ��M,ʹ
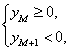 ��
��![]() ���t+s
���t+s![]() ��M��t+s+
��M��t+s+![]() .��M��N,��M=t+s,
.��M��N,��M=t+s,
��������Ȼ��M,����СֵΪt+s,ʹ�õ�n��Mʱ,xn��1�����.

 ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�