题目内容
有4个命题:①函数y=sin4x-cos4x的最小正周期是π;
②在同一坐标系中,函数y=sinx与y=x的图象有三个公共点;
③把函数y=3sin(2x+
)的图象向右平移
得到y=3sin2x的图象;
④函数y=sin(x-
)在[0,π]上是减函数.
其中真命题的序号是
②在同一坐标系中,函数y=sinx与y=x的图象有三个公共点;
③把函数y=3sin(2x+
| π |
| 6 |
| π |
| 6 |
④函数y=sin(x-
| π |
| 2 |
其中真命题的序号是
①
①
(填上所有真命题的序号).分析:由y=sin4x-cos4x=sin2x-cos2x=-cos2x,知它的最小正周期是T=
=π;在同一坐标系中,函数y=sinx与y=x的图象有两个公共点;把函数y=3sin(2x+
)的图象向右平移
,得到y=3sin[2(x-
)+
]=3sin(2x-
)的图象;函数y=sin(x-
)在[0,π]上是增函数.
| 2π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
解答:解:①∵y=sin4x-cos4x=sin2x-cos2x=-cos2x,
∴它的最小正周期是T=
=π,故①是真命题;
②在同一坐标系中,函数y=sinx与y=x的图象有一个公共点,故②是假命题;
③把函数y=3sin(2x+
)的图象向右平移
,
得到y=3sin[2(x-
)+
]=3sin(2x-
)的图象,故③是假命题;
④函数y=sin(x-
)在[0,π]上是增函数,故④是假命.
故答案为:①.
∴它的最小正周期是T=
| 2π |
| 2 |
②在同一坐标系中,函数y=sinx与y=x的图象有一个公共点,故②是假命题;
③把函数y=3sin(2x+
| π |
| 6 |
| π |
| 6 |
得到y=3sin[2(x-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
④函数y=sin(x-
| π |
| 2 |
故答案为:①.
点评:本题考查命题的真假判断和应用,是基础题.解题时要认真审题,仔细解答,注意三角函数性质的灵活运用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
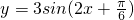 的图象向右平移
的图象向右平移 得到y=3sin2x的图象;
得到y=3sin2x的图象;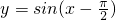 在[0,π]上是减函数.
在[0,π]上是减函数. 的图象向右平移
的图象向右平移 得到y=3sin2x的图象;
得到y=3sin2x的图象; 在[0,π]上是减函数.
在[0,π]上是减函数. 的图象向右平移
的图象向右平移 得到y=3sin2x的图象;
得到y=3sin2x的图象; 在[0,π]上是减函数.
在[0,π]上是减函数.