题目内容
在1,2,3,…,100中任意取三个数字构成等差数列,有几种不同的排法?
4900
先研究递增等差数列
首项为1:等差中项可从2取到50,共可组成49个等差数列
首项为2:等差中项可从3取到51,共可组成49个等差数列
首项为3:等差中项可从4取到51,共可组成48个等差数列
首项为4:等差中项可从5取到52,共可组成48个等差数列
首项为5:等差中项可从6取到52,共可组成47个等差数列
首项为6:等差中项可从7取到53,共可组成47个等差数列
首项为7:等差中项可从8取到53,共可组成46个等差数列
首项为8:等差中项可从9取到54,共可组成46个等差数列
……
由以上规律可知
首项为1、3、5、…97的递增等差数列的个数有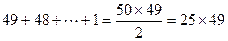 .
.
首项为2、4、6、…98的递增等差数列的个数有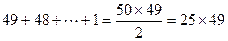 .
.
再添上递减数列
于是共有首项为1、3、5、…97的递增等差数列的个数有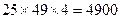 个.
个.
首项为1:等差中项可从2取到50,共可组成49个等差数列
首项为2:等差中项可从3取到51,共可组成49个等差数列
首项为3:等差中项可从4取到51,共可组成48个等差数列
首项为4:等差中项可从5取到52,共可组成48个等差数列
首项为5:等差中项可从6取到52,共可组成47个等差数列
首项为6:等差中项可从7取到53,共可组成47个等差数列
首项为7:等差中项可从8取到53,共可组成46个等差数列
首项为8:等差中项可从9取到54,共可组成46个等差数列
……
由以上规律可知
首项为1、3、5、…97的递增等差数列的个数有
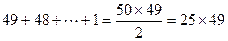 .
.首项为2、4、6、…98的递增等差数列的个数有
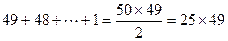 .
.再添上递减数列
于是共有首项为1、3、5、…97的递增等差数列的个数有
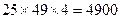 个.
个.
练习册系列答案
相关题目
 有4个元素,集合C满足条件:
有4个元素,集合C满足条件: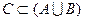 (2)C中含有3个元素; (3)
(2)C中含有3个元素; (3)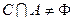
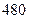 种
种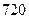 种
种 种
种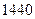 种
种 任取两个做除法,可得到不同的商的个数是 ( )
任取两个做除法,可得到不同的商的个数是 ( )
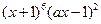 的展开式中
的展开式中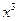 项的系数为
项的系数为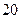 ,则实数
,则实数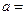 __________
__________ ,则
,则 .
.