题目内容
15.已知非零向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,且BC⊥OA,C为垂足,若$\overrightarrow{OC}$=λ$\overrightarrow{a}$(λ≠0),则实数λ等于( )| A. | $\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}{|}^{2}}$ | B. | $\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$ | C. | $\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}{|}^{2}}$ | D. | $\frac{|\overrightarrow{a}||\overrightarrow{b}|}{\overrightarrow{a}•\overrightarrow{b}}$ |
分析 由BC⊥OA便得到$\overrightarrow{BC}⊥\overrightarrow{OA}$,从而得到$\overrightarrow{BC}•\overrightarrow{OA}$=0,然后把$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=λ\overrightarrow{a}-\overrightarrow{b}$,$\overrightarrow{OA}=\overrightarrow{a}$带入进行数量积运算,从而可解出λ,从而找到正确选项.
解答 解:∵BC⊥OA;
∴$\overrightarrow{BC}•\overrightarrow{OA}=(\overrightarrow{OC}-\overrightarrow{OB})•\overrightarrow{OA}$=$(λ\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{a}=0$;
∴$λ{\overrightarrow{a}}^{2}=\overrightarrow{a}•\overrightarrow{b}$;
∴$λ=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}{|}^{2}}$.
故选A.
点评 考查两向量垂直的充要条件,数量积的运算,以及向量减法的几何意义.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
3.曲线|x|=|y|与直线x=3围成一个三角形区域,表示该区域的不等式组是( )
| A. | $\left\{{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{x≤3}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x-y≥0}\\{x+y≤0}\\{x≤3}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x-y≤0}\\{x+y≤0}\\{x≤3}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x-y≤0}\\{x+y≥0}\\{x≤3}\end{array}}\right.$ |
10.已知函数f(x)=x2-cosx,若当-π<x<π时,f(x1)<f(x2)恒成立,则下列结论一定成立的是( )
| A. | x1>x2 | B. | x1<x2 | C. | |x1|<|x2| | D. | |x1|>|x2| |
7.下列程序图中,输出的B是( )


| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | 0 | D. | $\sqrt{3}$ |
4.如图所示的程序框图的运行结果为S=35,那么判断框中应填入的关于k的条件是( )
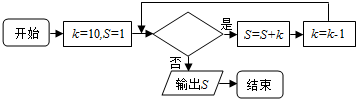

| A. | k>6 | B. | k≥6 | C. | k≥7 | D. | k>7 |