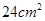题目内容
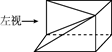
如图是一个空间几何体的正视图、侧视图、俯视图,如果正视图、侧视图所对应的三角形皆为边长为2的正三角形,俯视图对应的四边形为正方形,那么这个几何体的体积为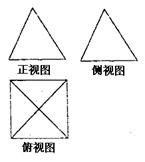
A.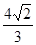 | B.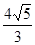 | C.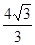 | D.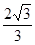 |
C
解析试题分析:该几何体是一正四棱锥,底面边长为2,,斜高为2,所以四棱锥的高为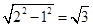 ,体积为
,体积为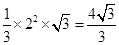 ,故选C。
,故选C。
考点:本题主要考查三视图,几何体特征,几何体体积计算。
点评:基础题,认识几何体的特征是解答此类题的关键。

练习册系列答案
相关题目
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD="2AB=6," 则该球的表面积为( )
A.16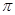 | B.24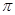 | C.48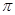 | D.32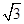  |
下列说法中正确的是
| A.棱柱的侧面可以是三角形 |
| B.正方体和长方体都是特殊的四棱柱 |
| C.所有的几何体的表面都能展成平面图形 |
| D.棱柱的各条棱都相等 |
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的体积为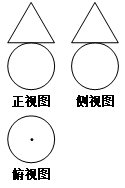
A.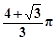 | B.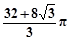 |
C.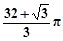 | D.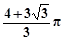 |
 的棱长为1,动点
的棱长为1,动点 在此正方体的表面上运动,且
在此正方体的表面上运动,且 ,记点
,记点 ,则函数
,则函数

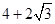 的圆柱形有盖容器中,放入一个半径为3的大球后再放入与球面、圆柱侧面及上底面均相切的小球,则放入的小球的个数最多的为
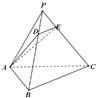
的圆柱形有盖容器中,放入一个半径为3的大球后再放入与球面、圆柱侧面及上底面均相切的小球,则放入的小球的个数最多的为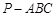 的底面是正三角形,各条侧棱均相等,
的底面是正三角形,各条侧棱均相等,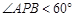 .设点
.设点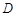 、
、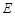 分别在线段
分别在线段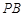 、
、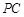 上,且
上,且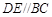 ,记
,记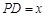 ,
,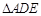 周长为
周长为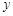 ,则
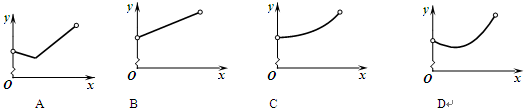
,则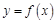 的图象可能是
的图象可能是