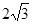题目内容
点 为圆
为圆 的弦的中点,则该弦所在直线的方程是( )
的弦的中点,则该弦所在直线的方程是( )
| A.x+y+1=0 | B.x+y-1=0 | C.x-y-1=0 | D.x-y+1=0 |
B
解析试题分析:点 为圆
为圆 的弦的中点,设圆心为
的弦的中点,设圆心为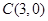 ,则该弦所在直线与PC垂直,故弦的斜率为
,则该弦所在直线与PC垂直,故弦的斜率为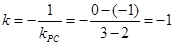 ,则由直线的点斜式可得弦方程为
,则由直线的点斜式可得弦方程为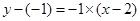 即
即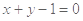 .
.
考点:圆的中点弦的直线方程,直线方程的点斜式.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知三条直线a,b,c,若a和b是异面直线,b和c是异面直线,那么直线a和c的位置关系是( )
| A.平行 | B.相交 | C.异面 | D.平行、相交或异面 |
已知直线l1: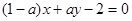 ,l2:
,l2: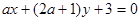 ,若
,若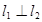 ,则a的值为
,则a的值为
| A.0或2 | B.0或一2 | C.2 | D.-2 |
直线 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )
A.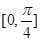 | B.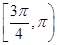 | C.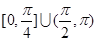 | D.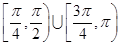 |
直线l经过点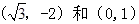 ,则它的倾斜角是( )
,则它的倾斜角是( )
| A.300 | B.600 | C.1500 | D.1200 |
过点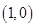 且与直线
且与直线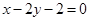 平行的直线方程是( )
平行的直线方程是( )
A.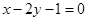 | B.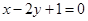 | C.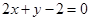 | D.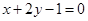 |
已知a,b满足a+2b=1,则直线ax+3y+b=0必过定点( )
A.(-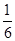 , ,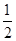 ) ) | B. (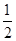 , ,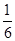 ) ) | C. (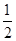 , - , -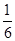 ) ) | D. (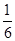 , - , -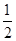 ) ) |
当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心,半径为的圆的方程为( )
| A.x2+y2-2x+4y=0 |
| B.x2+y2+2x+4y=0 |
| C.x2+y2+2x-4y=0 |
| D.x2+y2-2x-4y=0 |
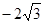 B.0 C.
B.0 C.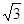 D.
D.