题目内容
计算:(1)设a,b∈R,
 (i为虚数单位),求a+b的值.
(i为虚数单位),求a+b的值.(2)若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有m种.求m的值.
【答案】分析:(1)由题意可对复数代数式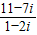 分子与分母都乘以1+2i,再进行化简计算,再由复数相等的条件求出a和b的值,即可得答案;
分子与分母都乘以1+2i,再进行化简计算,再由复数相等的条件求出a和b的值,即可得答案;
(2)根据题意需要分三类计算:①4个偶数;②2个奇数,2个偶数;③4个奇数,再由组合公式求解即可.
解答:解:(1)∵a+bi=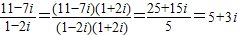 ,
,
∴a=5,b=3,a+b=8.;
(2)根据题意偶数为2、4、6、8,奇数为1、3、5、7、9,
需要分三类计算:①4个偶数;②2个奇数,2个偶数;③4个奇数,
则符合题意的取法共有:
m=C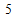 C
C +C
+C C
C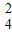 +C
+C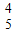 C
C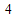 =1+60+5=66(种)
=1+60+5=66(种)
点评:本题考查复数代数形式的乘除运算和组合公式,解题的关键是分子分母都乘以分母的共轭复数和明确进行分类,复数的四则运算是复数考查的重要内容,要熟练掌握.
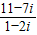 分子与分母都乘以1+2i,再进行化简计算,再由复数相等的条件求出a和b的值,即可得答案;
分子与分母都乘以1+2i,再进行化简计算,再由复数相等的条件求出a和b的值,即可得答案;(2)根据题意需要分三类计算:①4个偶数;②2个奇数,2个偶数;③4个奇数,再由组合公式求解即可.
解答:解:(1)∵a+bi=
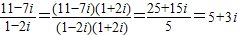 ,
,∴a=5,b=3,a+b=8.;
(2)根据题意偶数为2、4、6、8,奇数为1、3、5、7、9,
需要分三类计算:①4个偶数;②2个奇数,2个偶数;③4个奇数,
则符合题意的取法共有:
m=C
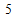 C
C +C
+C C
C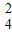 +C
+C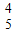 C
C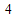 =1+60+5=66(种)
=1+60+5=66(种)点评:本题考查复数代数形式的乘除运算和组合公式,解题的关键是分子分母都乘以分母的共轭复数和明确进行分类,复数的四则运算是复数考查的重要内容,要熟练掌握.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目