题目内容
（1）计算：
-(
)0+0.25
×(
)-4；
（2）解关于x的方程：log5(x+1)-log
(x-3)=1．
| 3 | (-4)3 |
| 1 |
| 2 |
| 1 |
| 2 |
| -1 | ||
|
（2）解关于x的方程：log5(x+1)-log
| 1 |
| 5 |
分析：（1）根据分数指数幂运算法则进行化简即可．
（2）利用对数函数的性质和对数的运算法则进行计算即可．
（2）利用对数函数的性质和对数的运算法则进行计算即可．
解答：解：（1）原式=-4-1+
×(
)4=-3；
（2）原方程化为 log5（x+1）+log5（x-3）=log55，
从而（x+1）（x-3）=5，解得x=-2或x=4，
经检验，x=-2不合题意，
故方程的解为x=4．
| 1 |
| 2 |
| 2 |
（2）原方程化为 log5（x+1）+log5（x-3）=log55，
从而（x+1）（x-3）=5，解得x=-2或x=4，
经检验，x=-2不合题意，
故方程的解为x=4．
点评：本题主要考查分数指数幂和对数的运算，要求熟练掌握分数指数幂和对数的运算法则．
练习册系列答案
相关题目
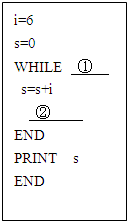图中程序是计算2+3+4+5+6的值的程序．在WHILE后的①处和在s=s+i之后的②处所就填写的语句可以是（ ）
;
;
;
.