题目内容
函数 的图象关于直线
的图象关于直线 对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 .
对称,它的最小正周期为π.则函数y=f(x)图象上离坐标原点O最近的对称中心是 .
【答案】分析:先根据函数的最小正周期求出ω的值,因为函数的对称轴为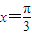 ,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.
,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.
解答:解:函数f(x)=Asin(ωx+∅)的周期T= =π,∴ω=2
=π,∴ω=2
∵函数f(x)=Asin(2x+∅)的图象关于直线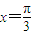 对称,∴f(0)=f(
对称,∴f(0)=f( )
)
即Asin∅=Asin(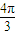 +∅),化简得,sin∅=-
+∅),化简得,sin∅=- cos∅-
cos∅- sinφ
sinφ
 sin∅=-
sin∅=- cos∅,tan∅=-
cos∅,tan∅=-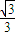 ,
,
又∵|∅|<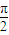 ,∴∅=-
,∴∅=-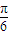 ,∴f(x)=Asin(2x-
,∴f(x)=Asin(2x-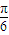 )
)
令2x- =kπ,k∈Z,解得,x=
=kπ,k∈Z,解得,x= ,k∈Z,
,k∈Z,
∴函数y=f(x)图象的对称中心是(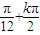 ,0),k∈Z
,0),k∈Z
其中,离坐标原点O最近的对称中心是(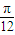 ,0)
,0)
故答案为(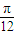 ,0)
,0)
点评:本题主要考查y=Asin(ωx+∅)的图象与性质,解题时借助基本的正弦函数的图象和性质.
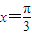 ,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.
,所以在对称轴左右两侧取关于对称轴对称的两个x的值,则其函数值相等,就可求出∅的值,得到函数的解析式.再根据基本正弦函数的对称中心求出此函数的对称中心即可.解答:解:函数f(x)=Asin(ωx+∅)的周期T=
 =π,∴ω=2
=π,∴ω=2∵函数f(x)=Asin(2x+∅)的图象关于直线
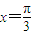 对称,∴f(0)=f(
对称,∴f(0)=f( )
)即Asin∅=Asin(
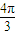 +∅),化简得,sin∅=-
+∅),化简得,sin∅=- cos∅-
cos∅- sinφ
sinφ sin∅=-
sin∅=- cos∅,tan∅=-
cos∅,tan∅=-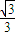 ,
,又∵|∅|<
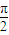 ,∴∅=-
,∴∅=-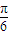 ,∴f(x)=Asin(2x-
,∴f(x)=Asin(2x-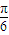 )
)令2x-
 =kπ,k∈Z,解得,x=
=kπ,k∈Z,解得,x= ,k∈Z,
,k∈Z,∴函数y=f(x)图象的对称中心是(
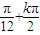 ,0),k∈Z
,0),k∈Z其中,离坐标原点O最近的对称中心是(
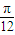 ,0)
,0)故答案为(
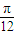 ,0)
,0)点评:本题主要考查y=Asin(ωx+∅)的图象与性质,解题时借助基本的正弦函数的图象和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的实数解的个数为1;
的实数解的个数为1;
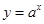 的图象可以由函数
的图象可以由函数 (其中
(其中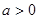 且
且 )平移得到;
)平移得到;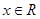 ,有
,有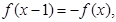 则
则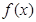 的周期为2;
的周期为2; 与函数
与函数 的图象关于直线
的图象关于直线 对称.
对称. 满足条件
满足条件 ,且函数
,且函数 是奇函数,由下列四个命题中不正确的是 ( )
是奇函数,由下列四个命题中不正确的是 ( ) 的图象关于点
的图象关于点 对称
对称 对轴
对轴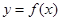 满足条件
满足条件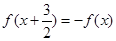 ,且函数
,且函数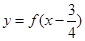 是奇函数,由下列四个命题中不正确的是 ( )
是奇函数,由下列四个命题中不正确的是 ( )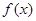 的图象关于点
的图象关于点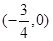 对称
对称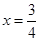 对轴
对轴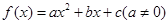 的图象关于直线
的图象关于直线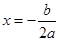 对称。据此可推测,对任意的非零实数
对称。据此可推测,对任意的非零实数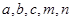 ,关于
,关于 的方程
的方程 的解集都不可能是(
)
的解集都不可能是(
) B
B
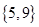 C
C
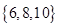 D
D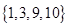
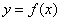 满足条件
满足条件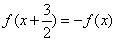 ,且函数
,且函数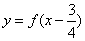 是奇函数,由下列四个命题中不正确的是 ( )
是奇函数,由下列四个命题中不正确的是 ( )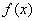 的图象关于点
的图象关于点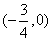 对称
对称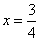 对轴
对轴