题目内容
(上海春卷22)在平面上,给定非零向量| b |
| a |
| a′ |
| a |
2(
| ||||
|
| b |
(1)若
| a |
| b |
| a′ |
(2)若
| b |
| a |
| a′ |
分析:(1)把已知
=
-
,
=(2,3),
=(-1,3)代入,利用坐标表示即可
(2)设
=(x,y),
=(x′,y′),由
=
-
可先找出x、yx′、y′之间的关系,向量
的终点在直线Ax+By+C=0上,把向量
的坐标代入,然后代换成关于
的坐标即可
| a′ |
| a |
2(
| ||||
|
| b |
| a |
| b |
(2)设
| a |
| a′ |
| a′ |
| a |
2(
| ||||
|
| b |
| a |
| a |
| a′ |
解答:解:(1)
=
-
=(2,3)-
• (-1,3)=(
,-
)
(2)设
=(x,y),
=(x′,y′)则
(x′,y′)=(x,y)-
(2x+y)•(2,1)=(-
x-
y,-
x+
y)
∴
于是
故A(-
x′-
y′ )+B(-
x′ +
y′)+C=0
从而-
(3A+4B)x′+
(-4A+3B)y′+C=0
由于A、B不全为零,所以3A+4B、-4A+3B也不全为零
于是
的终点在直线-
(3A+4B)x+
(-4A+3B)y+C=0上
| a′ |
| a |
2(
| ||||
|
|
| b |
| 2×(-2+9) |
| 10 |
| 17 |
| 5 |
| 6 |
| 5 |
(2)设
| a |
| a′ |
(x′,y′)=(x,y)-
| 2 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
∴
|
|
故A(-
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
从而-
| 1 |
| 5 |
| 1 |
| 5 |
由于A、B不全为零,所以3A+4B、-4A+3B也不全为零
于是
| a′ |
| 1 |
| 5 |
| 1 |
| 5 |
点评:本题主要考查了向量的数量积的坐标表示,向量的基本运算,判断点在直线上,属于基本方法的考查.

练习册系列答案
相关题目
 ,对任意向量
,对任意向量 ,定义
,定义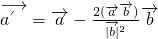 .
.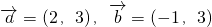 ,求
,求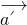 ;
;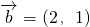 ,证明:若位置向量
,证明:若位置向量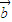 ,对任意向量
,对任意向量 ,定义
,定义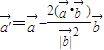 .
. ,求
,求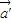 ;
;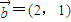 ,证明:若位置向量
,证明:若位置向量 的终点在直线Ax+By+C=0上,则位置向量
的终点在直线Ax+By+C=0上,则位置向量 的终点也在一条直线上.
的终点也在一条直线上.