题目内容
命题


 命题
命题
 ,双曲线
,双曲线 的离心率为
的离心率为 ,则下面结论正确的是( )
,则下面结论正确的是( )
A. 是假命题 是假命题 | B. 是真命题 是真命题 | C.  是假命题 是假命题 | D.  是真命题 是真命题 |
D
解析试题分析:因为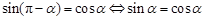 ,当
,当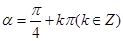 时,满足
时,满足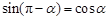 ,故
,故 真;对
真;对 时,双曲线
时,双曲线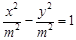 的离心率
的离心率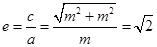 ,所以
,所以 也正确,由复合命题的真值表可知
也正确,由复合命题的真值表可知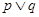 为真,
为真,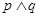 为真,
为真, 为假,故选D.
为假,故选D.
考点:逻辑联结词.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知向量 ,
,  ,则
,则 是
是 的 ( )
的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知函数 则
则 是
是 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“ ”是“直线
”是“直线 与直线
与直线 互相平行”的( )
互相平行”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“ ”是“
”是“ ”的
”的
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知条件 ,条件
,条件 ,则
,则 是
是 成立的( )
成立的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在一次跳伞训练中,甲、乙两位学员各跳一次.设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为( )
A.( p)∨( p)∨( q) q) | B.p∨( q) q) |
C.( p)∧( p)∧( q) q) | D.p∨q |
下列说法中,不正确的是( )
A.命题p:?x∈R,sinx≤1,则 p:?x∈R,sinx>1 p:?x∈R,sinx>1 |
B.在△ABC中,“A>30°”是“sinA> ”的必要不充分条件 ”的必要不充分条件 |
C.命题p:点( ,0)为函数f(x)=tan(2x+ ,0)为函数f(x)=tan(2x+ )的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则( )的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则( p)∨( p)∨( q)为真命题 q)为真命题 |
| D.命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题为真命题 |
 在R上为增函数,p2:函数
在R上为增函数,p2:函数 在R上为减函数,则在命题
在R上为减函数,则在命题 和
和 中,真命题是 ( )
中,真命题是 ( )


