题目内容
将直线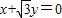
绕原点按顺时针方向旋转30°，所得直线与圆（x-2）2+y2=3的位置关系是 ．
【答案】分析：先求出所得直线方程，再计算 圆心到所得直线的距离，将此距离与圆的半径比较．
解答：解：直线
斜率为-
，倾斜角150，绕原点按顺时针方向旋转30°后，
得到的直线倾斜角120，斜率为-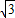
，∴所得直线方程为：y=-
x，即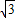
x+y=0，
圆心到所得直线的距离为：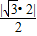
=
=半径
，
所得直线与圆（x-2）2+y2=3的位置关系是相切．
点评：本题考查直线和圆的位置关系．
解答：解：直线
斜率为-，倾斜角150，绕原点按顺时针方向旋转30°后，得到的直线倾斜角120，斜率为-
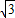，∴所得直线方程为：y=-x，即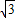x+y=0，圆心到所得直线的距离为：
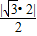==半径，所得直线与圆（x-2）2+y2=3的位置关系是相切．
点评：本题考查直线和圆的位置关系．
练习册系列答案
相关题目
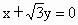绕原点按顺时针方向旋转30°，所得直线与圆
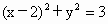的位置关系是
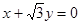绕原点按顺时针方向旋转30°，所得直线与圆(x－2)2＋y2＝3的位置关系是
绕原点按顺时针方向旋转
，所得直线与圆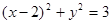
的位置关系是 
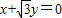绕原点按顺时针方向旋转30°，所得直线与圆（x-2）2+y2=3的位置关系是 ．