题目内容
如果函数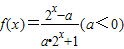 是奇函数,则函数y=f(x)的值域是( )
是奇函数,则函数y=f(x)的值域是( )A.[-1,1]
B.(-1,1]
C.(-1,1]
D.(-∞,-1)∪(1,+∞)
【答案】分析:根据函数为奇函数,由奇函数定义求出a的值,然后通过变形使得函数式变为只是分母含有未知量的函数,最后根据取值变化求出函数值域.
解答:解:∵函数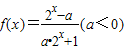 是奇函数,
是奇函数,
所以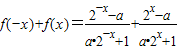 =
= 恒成立,
恒成立,
∴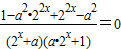
即1-a2•22x+22x-a2=0,
也就是(1-a2)(1+22x)=0恒成立,
即1-a2=0
∴a=-1,或a=1(舍),
故a=-1,∴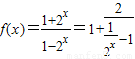 ,
,
∵2x>0,∴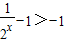 ,
,
∴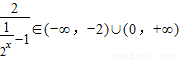 ,
,
∴f(x)∈(-∞,-1)∪(1,+∞),
∴函数的值域为(-∞,-1)∪(1,+∞).
故选D.
点评:本题考查了函数奇偶性的判断及应用,考查了运用函数奇偶性求函数解析式的方法,求函数值域时运用了极限思想,是容易出错的地方.
解答:解:∵函数
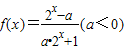 是奇函数,
是奇函数,所以
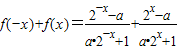 =
= 恒成立,
恒成立,∴
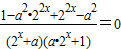
即1-a2•22x+22x-a2=0,
也就是(1-a2)(1+22x)=0恒成立,
即1-a2=0
∴a=-1,或a=1(舍),
故a=-1,∴
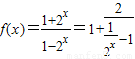 ,
,∵2x>0,∴
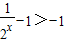 ,
,∴
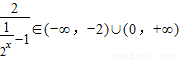 ,
,∴f(x)∈(-∞,-1)∪(1,+∞),
∴函数的值域为(-∞,-1)∪(1,+∞).
故选D.
点评:本题考查了函数奇偶性的判断及应用,考查了运用函数奇偶性求函数解析式的方法,求函数值域时运用了极限思想,是容易出错的地方.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
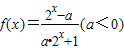 是奇函数,则函数y=f(x)的值域是( )
是奇函数,则函数y=f(x)的值域是( )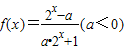 是奇函数,则函数y=f(x)的值域是( )
是奇函数,则函数y=f(x)的值域是( )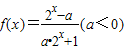 是奇函数,则函数y=f(x)的值域是( )
是奇函数,则函数y=f(x)的值域是( )
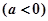 是奇函数,则函数
是奇函数,则函数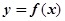 的值域是
的值域是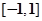 B.
B.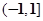 C.
C. D.
D.