题目内容
．已知函数
， 
（1）若函数
在
上是减函数，求实数
的取值范围
（2）令
，是否存在实数，当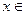
（
是自然常数）时，函数
的最小值是3，若存在，求出的值；若不存在，说明理由
（3）当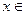时，证明： 
解：（1）
在上恒成立
令 
，有
得
得
（2）假设存在实数，使
（
）有最小值3，
①当
时，在
上单调递减，
，
（舍去），
②当
时，在
上单调递减，在
上单调递增
，
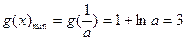，满足条件
③当
时，在上单调递减，，（舍去），
综上，存在实数，使得当时
有最小值3
（3）令
，由（2）知
．令
，
当
时，
，
在上单调递增
∴
即
解析
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
已知函数f(x)=
+
的定义域是（ ）
| 1-x2 |
| x2-1 |
| A、[-1，1] |
| B、{-1，1} |
| C、（-1，1） |
| D、（-∞，-1]∪[1，+∞） |