题目内容
函数f(x)=7+ax-3 (a>0,a≠1)的图象恒过定点P,则定点P的坐标为
| A.(3,3) | B.(3,2) | C.(3,8) | D.(3,7) |
C
析:由题意令x-3=0,解得x=3,再代入函数解析式求出y的值,得到函数f(x)图象恒过的定点,然后根据原函数与反函数图象的关系可得到结论.
解答:解:令x-3=0,解得x=3,则x=3时,函数y=a0+7=8,
即函数f(x)图象恒过一个定点(3,8).
故选C.
点评:本题主要考查了指数函数的单调性与特殊点,以及原函数与反函数图象的关系,属于基础题.
解答:解:令x-3=0,解得x=3,则x=3时,函数y=a0+7=8,
即函数f(x)图象恒过一个定点(3,8).
故选C.
点评:本题主要考查了指数函数的单调性与特殊点,以及原函数与反函数图象的关系,属于基础题.

练习册系列答案
相关题目
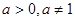 ,则函数
,则函数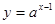 的图象一定过点 ( )
的图象一定过点 ( )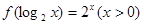 ,则
,则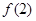 的值是( )
的值是( )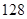
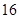
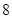
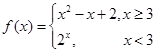 ,若
,若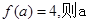 的值等于
的值等于  ,市场价微机桌每张为150元,鼠标垫每个为5元,该培训机构老板联系了两家商场甲和乙,由于用货量大,这
,市场价微机桌每张为150元,鼠标垫每个为5元,该培训机构老板联系了两家商场甲和乙,由于用货量大,这 两家商场都给出了优惠条件
两家商场都给出了优惠条件 60张,鼠标垫
60张,鼠标垫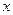 个(
个( ),如果两种商品只能在一家购买,请你帮助该培训机构老板选择在哪一家商场买更省钱?
),如果两种商品只能在一家购买,请你帮助该培训机构老板选择在哪一家商场买更省钱?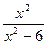 ,
, 定义域;
定义域;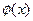 ] = lgx,求
] = lgx,求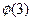 的值。
的值。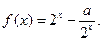 将
将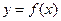 的图象向右平移2个单位,得到
的图象向右平移2个单位,得到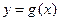 的图象.
的图象.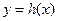 与函数
与函数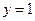 对称,求函数
对称,求函数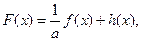 已知
已知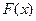 的最小值是
的最小值是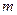 ,且
,且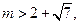 求实数
求实数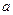 的
的 取值范围.
取值范围.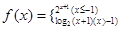 ,若
,若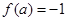 ,则
,则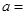 ( )
( )