题目内容
设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围是 ( ).
A. | B.[-1,0] | C.(-∞,-2] | D. |
A
解析

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知函数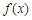 的定义域为R,若存在常数
的定义域为R,若存在常数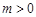 ,对任意
,对任意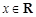 ,有
,有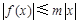 ,则称
,则称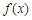
为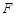 函数.给出下列函数:①
函数.给出下列函数:①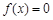 ; ②
; ②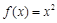 ; ③
; ③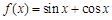 ;
;
④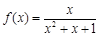 ; ⑤
; ⑤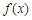 是定义在R上的奇函数,且满足对一切实数
是定义在R上的奇函数,且满足对一切实数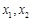 均
均
有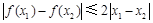 .其中是
.其中是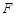 函数的序号为( )
函数的序号为( )
| A.①②④ | B.②③④ | C.①④⑤ | D.①②⑤ |
下列说法正确的是( )
A.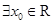 , ,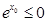 |
B.对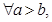 则 则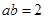 , ,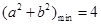 |
C.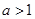 , ,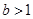 是 是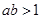 的充分条件 的充分条件 |
D.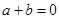 的充要条件是 的充要条件是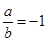 |
已知幂函数 的图像过点
的图像过点 ,若
,若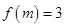 ,则实数
,则实数 的值为( )
的值为( )
A. | B.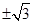 | C.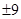 | D.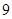 |
设函数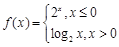 ,若对任意给定的
,若对任意给定的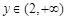 ,都存在唯一的
,都存在唯一的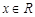 ,满足
,满足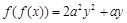 ,则正实数
,则正实数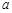 的最小值是( )
的最小值是( )
A.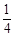 | B.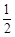 | C.2 | D.4 |
若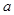 是函数
是函数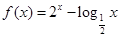 的零点,若
的零点,若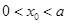 ,则
,则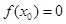 的值满足( )
的值满足( )
A.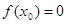 | B.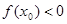 |
C.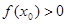 | D.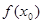 的符号不确定 的符号不确定 |
若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)= ,则f(x)的单调递减区间是( )
,则f(x)的单调递减区间是( )
| A.(-∞,2] | B.[2,+∞) |
| C.[-2,+∞) | D.(-∞,-2] |
已知函数f(x)=2x+1,x∈N*.若?x0,n∈N*,使f(x0)+f(x0+1)+…+f(x0+n)=63成立,则称(x0,n)为函数f(x)的一个“生成点”.则函数f(x)的“生成点”共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
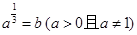 ,则( )
,则( )
A.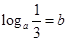 | B.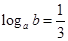 | C.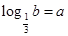 | D.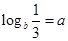 |