Question

解不等式2≤|1-4x|＜7.

Answer 1

分析：由于原不等式中含两个不等号,既要满足|1-4x|＜7,又要满足|1-4x|≥2,故可化为不等式组求解.

解法一：原不等式可化为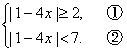

解不等式①,得{x|x≤-,或x≥};

解不等式②,得{x|-＜x＜2},

所以原不等式的解集是{x|x≤-,或x≥}∩{x|-＜x＜2}={x|-＜x≤-或≤x＜2}

=(-,-］∪［,2).

解法二：根据绝对值的定义,有|1-4x|=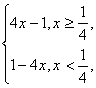

所以原不等式是下列两个不等式组的并集.

(1)(2)

由(1)得{x|≤x＜2};由(2)得{x|-＜x≤-}.

∴原不等式的解集是{x|-＜x≤-}∪{x|≤x＜2}=(-］∪［,2).