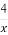题目内容
已知函数f(x)=x3+x-16.
(1)求曲线y=f(x)在点(2,-6)处的切线方程.
(2)如果曲线y=f(x)的某一切线与直线y=- x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.
(1) y=13x-32 (2) 切点坐标为(1,-14)或(-1,-18) y=4x-18或y=4x-14
【解析】(1)可判定点(2,-6)在曲线y=f(x)上.
∵f'(x)=(x3+x-16)'=3x2+1,
∴在点(2,-6)处的切线的斜率为k=f'(2)=13,
∴切线的方程为y=13(x-2)+(-6),
即y=13x-32.
(2)∵切线与直线y=-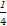 x+3垂直,
x+3垂直,
∴切线的斜率k=4.
设切点的坐标为(x0,y0),则f'(x0)=3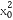 +1=4,
+1=4,
∴x0=±1,
∴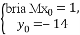 或
或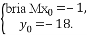
∴切点坐标为(1,-14)或(-1,-18),
切线方程为y=4(x-1)-14或y=4(x+1)-18.
即y=4x-18或y=4x-14.

练习册系列答案
相关题目