题目内容
下列说法错误的个数为( )①命题“若b2-4ac>0,则一元二次方程ax2+bx+c=0有实根”的逆否命题是真命题
②“x2-3x+2=0”是“x=2”的必要不充分条件
③命题“若xy=0,则x,y中至少有一个为零”的否定是:“若xy≠0,则x,y都不为零”
④命题p:?x∈R,使得x2+x+1<0;则¬p:?x∈R,均有x2+x+1>0
⑤若命题¬p为真,¬q为假,则命题¬p∧q为真,p∨¬q为假.
A.1
B.2
C.3
D.4
【答案】分析:①由原命题是真命题,知它的逆否命题是真命题;②∵“x2-3x+2=0”⇒“x=2,或x=1”,“x=2”⇒“x2-3x+2=0”;③命题“若xy=0,则x,y中至少有一个为零”的否定是:“若xy≠0,则x,y都不为零”;④命题p:?x∈R,使得x2+x+1<0;则¬p:?x∈R,均有x2+x+1≥0;⑤若命题¬p为真,¬q为假,则命题¬p∧q为真,p∨¬q为真.
解答:解:①∵命题“若b2-4ac>0,则一元二次方程ax2+bx+c=0有实根”是真命题,
∴它的逆否命题是真命题,故①正确;
②∵“x2-3x+2=0”⇒“x=2,或x=1”,“x=2”⇒“x2-3x+2=0”,
∴“x2-3x+2=0”是“x=2”的必要不充分条件,故②正确;
③命题“若xy=0,则x,y中至少有一个为零”的否定是:“若xy≠0,则x,y都不为零”,
故③正确;
④命题p:?x∈R,使得x2+x+1<0;则¬p:?x∈R,均有x2+x+1≥0,
故④不正确;
⑤若命题¬p为真,¬q为假,则命题¬p∧q为真,p∨¬q为真,
故⑤不正确.
故选B.
点评:本题考查命题的真假判断与应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
解答:解:①∵命题“若b2-4ac>0,则一元二次方程ax2+bx+c=0有实根”是真命题,
∴它的逆否命题是真命题,故①正确;
②∵“x2-3x+2=0”⇒“x=2,或x=1”,“x=2”⇒“x2-3x+2=0”,
∴“x2-3x+2=0”是“x=2”的必要不充分条件,故②正确;
③命题“若xy=0,则x,y中至少有一个为零”的否定是:“若xy≠0,则x,y都不为零”,
故③正确;
④命题p:?x∈R,使得x2+x+1<0;则¬p:?x∈R,均有x2+x+1≥0,
故④不正确;
⑤若命题¬p为真,¬q为假,则命题¬p∧q为真,p∨¬q为真,
故⑤不正确.
故选B.
点评:本题考查命题的真假判断与应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则一元二次方程
,则一元二次方程 有实根”的逆否命题是真命题
有实根”的逆否命题是真命题 0;则
0;则 p:∀x∈R,均有x2+x+1
p:∀x∈R,均有x2+x+1 0
0 为假,则命题
为假,则命题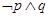 为真,
为真, 为假
为假