题目内容
已知等差数列40,37,34,…前n项和为Sn,则使Sn最大的正整数n=( )
分析:由等差数列40,37,34,…可求出数列的首项和公差,进而求出数列正项和负项的分界点,进而得到答案.
解答:解:等差数列40,37,34,…是以40为首项,-3为公差的等差数列
故an中,n≤14时,an>0,n>14时,an<0,
故使Sn最大的正整数n=14
故选C
故an中,n≤14时,an>0,n>14时,an<0,
故使Sn最大的正整数n=14
故选C
点评:本题考查的知识点是等差数列的前n项和的最值,求出数列正项和负项的分界点,是解答的关键.

练习册系列答案
相关题目
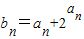 (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn.