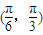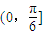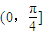题目内容
已知两线段a=2,b=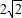 ,若以a,b为边作三角形,则a边所对的角A的取值范围为( )
,若以a,b为边作三角形,则a边所对的角A的取值范围为( )A.
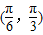
B.
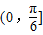
C.

D.
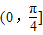
【答案】分析:可将△ABC的另一边设为c,通过余弦定理,将角A转化为变量c的函数,应用基本不等式解决.
解答:解:设△ABC的另一边为c,a,b,c各边所对的角分别为A、B、C,
由余弦定理可得: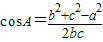 =
=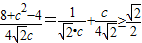 (当且仅当
(当且仅当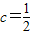 时取“=”);又A>0,
时取“=”);又A>0,
∴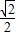 ≤cosA<1,
≤cosA<1,
故选D.
点评:本题考查余弦定理,难点在于应用余弦定理后转化为含变量c的关系式,再应用基本不等式,跨度较大,属于中档题.
解答:解:设△ABC的另一边为c,a,b,c各边所对的角分别为A、B、C,
由余弦定理可得:
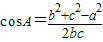 =
=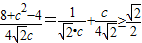 (当且仅当
(当且仅当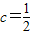 时取“=”);又A>0,
时取“=”);又A>0,∴
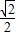 ≤cosA<1,
≤cosA<1,故选D.
点评:本题考查余弦定理,难点在于应用余弦定理后转化为含变量c的关系式,再应用基本不等式,跨度较大,属于中档题.

练习册系列答案
相关题目
 ,若以a,b为边作三角形,则a边所对的角A的取值范围为( )
,若以a,b为边作三角形,则a边所对的角A的取值范围为( )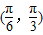
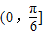
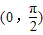
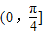
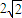 ,若以a,b为边作三角形,则a边所对的角A的取值范围为( )
,若以a,b为边作三角形,则a边所对的角A的取值范围为( )