题目内容
(2006
北京海淀模拟)已知A(-2,0)、B(2,0),点C、D满足 ,
, .
.
(1)
求点D的轨迹方程;(2)
过点A作直线l交以A、B为焦点的椭圆于M、N两点,线段MN的中点到y轴的距离为 ,且直线l与点D的轨迹相切,求该椭圆的方程.
,且直线l与点D的轨迹相切,求该椭圆的方程.
答案:略
解析:
解析:
|
解析: (1)设C、D点的坐标分别为 ,D(x,y),则 ,D(x,y),则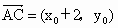 , ,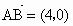 ,则 ,则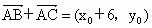 , ,
由 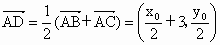 . .
又 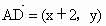 ,故 ,故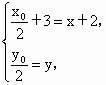
解得 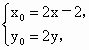
代入  得 得 ,即为所求点D的轨迹方程. ,即为所求点D的轨迹方程.
(2) 易知直线l与x轴不垂直,设直线l的方程为y=k(x+2). ①又设椭圆方程为  . ② . ②
因为直线 l与圆 相切,故 相切,故 ,解得 ,解得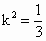 . .
将①代入②整理得  , ,
而 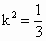 ,即 ,即 , ,
设 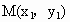 , ,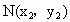 ,则 ,则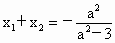 , ,
由题意有 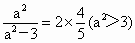 ,求得 ,求得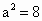 .经检验,此时Δ>0, .经检验,此时Δ>0,
故所求的椭圆方程为 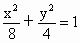 . . |

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
(2006
北京海淀模拟)若直线l∶ax+by=1与圆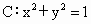 有两个不同交点,则点P(a,b)与圆C的位置关系是
有两个不同交点,则点P(a,b)与圆C的位置关系是
[
]|
A .点在圆上 |
B .点在圆内 |
|
C .点在圆外 |
D .不能确定 |
 ,满足
,满足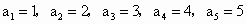 .当n≥5时,
.当n≥5时, .若数列
.若数列 满足
满足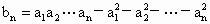 .
.
 ;
;
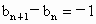 ;
;
 .
. ,给出下列四个命题
,给出下列四个命题
 ;
;
 ;
;
 中心对称;
中心对称;
 中,
中,

 、
、 的中点.
的中点.
 的距离;
的距离;
 的大小;
的大小;
 ?若存在,确定其位置并证明结论;若不存在,说明理由.
?若存在,确定其位置并证明结论;若不存在,说明理由.
