题目内容
由一条曲线 与直线
与直线 以及
以及 轴所围成的曲边梯形的面积是______。
轴所围成的曲边梯形的面积是______。
 与直线
与直线 以及
以及 轴所围成的曲边梯形的面积是______。
轴所围成的曲边梯形的面积是______。ln2
分析:先根据题意画出区域,然后依据图形得到积分上限为1,积分下限为
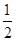 ,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.
,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.解答:解:先根据题意画出图形,得到积分上下限
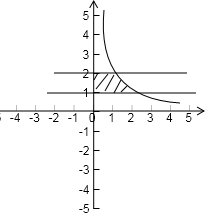
函数f(x)=
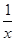 的图象与直线y=1,y=2以及y轴所围成的曲边梯形的面积是∫
的图象与直线y=1,y=2以及y轴所围成的曲边梯形的面积是∫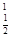 (
(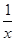 -1)dx+
-1)dx+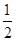
而∫
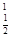 (
(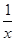 -1)dx+
-1)dx+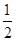
=(lnx-x)|
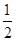
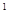 =ln2-
=ln2-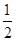 +
+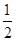 =ln2
=ln2∴曲边梯形的面积是ln2
故答案为:ln2.
点评:考查学生会求出原函数的能力,以及会利用定积分求图形面积的能力,同时考查了数形结合的思想,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 ( )
( )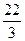
 (2)
(2)  (3)
(3)

 的值为()
的值为()


 =
= ,则实数a等于( )
,则实数a等于( )

 的值是**********
的值是**********  ,若
,若 ,则
,则 .
. ,y=
,y= 围成的封闭图形面积为( )
围成的封闭图形面积为( )


