题目内容
定义运算: ,将函数
,将函数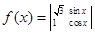 的图象向左平移
的图象向左平移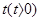 个单位,所得图象对应的函数为偶函数,则
个单位,所得图象对应的函数为偶函数,则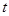 的最小值为( )
的最小值为( )
A.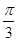 | B.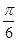 | C.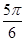 | D.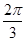 |
C
解析考点:二阶矩阵;函数奇偶性的性质.
专题:计算题.
分析:先用行列式展开法则求出f(x),再由函数的平移公式能够得到f(x+m),然后由偶函数的性质求出m的最小值.
解答:解:f(x)= cosx-sinx=2cos(x+
cosx-sinx=2cos(x+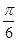 ),
),
图象向左平移m(m>0)个单位,
得f(x+m)=2cos(x+m+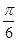 ),
),
则当n取得最小值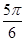 时,函数为偶函数.
时,函数为偶函数.
故选C.
点评:本题考查二阶行列式的展开法则,解题时要注意函数的平移和偶函数的合理运用.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
函数 为奇函数,
为奇函数, 的反函数,若
的反函数,若 则
则 =( )
=( )
A. | B.1 | C. | D.2 |
设函数y=f(x)存在反函数y= ,且函数
,且函数 的图象过点(1,2),则函数
的图象过点(1,2),则函数 的图象一定过点 ( )
的图象一定过点 ( )
| A.(-1,2) | B.(2,0) | C.(1,2) | D.(2,1) |
若定义在R上的偶函数 ,且当
,且当 则函数
则函数 的零点个数是 ( )
的零点个数是 ( )
| A.多于4个 | B.4个 | C.3个 | D.2个 |
定义两种运算: ,
,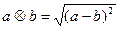 ,
,
则函数
| A.是奇函数 | B.是偶函数 |
| C.既是奇函数又是偶函数 | D.既不是奇函数又不是偶函数 |
函数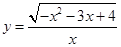 的定义域为( )
的定义域为( )
A. | B. | C. | D.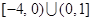 |
函数 在x=1处的切线方程为
在x=1处的切线方程为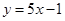 ,则a,c的值分别为
,则a,c的值分别为
A.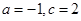 | B.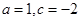 | C.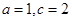 | D.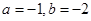 |
已知函数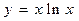 ,则其在点x=1处的切线方程是( )
,则其在点x=1处的切线方程是( )
A.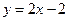 | B. | C.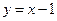 | D. |
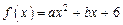 满足条件
满足条件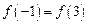 ,则
,则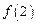 的值为( )
的值为( )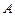 .5
.5 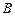 .6
.6 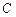 .8
.8 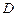 .与
.与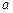 ,
, 值有关
值有关