题目内容
已知函数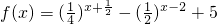 .
.
(Ⅰ)解不等式f(x)>5;
(Ⅱ)求函数f(x)的单调区间.
 解:(Ⅰ)∵
解:(Ⅰ)∵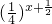 -
- +5>5,
+5>5,∴
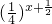 >
> .…(2分)
.…(2分)所以
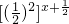 >
> .
.即
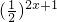 >
> .…(4分)
.…(4分)从而2x+1<x-2,解之得x<-3.…(7分)
所以不等式f(x)>5的解集为(-∞,-3).…(8分)
(Ⅱ)∵
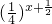 -
- +5
+5=
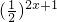 -
- +5
+5=
 •
•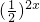 -
-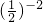 •
• +5
+5=
 •
• -4•
-4• +5…(10分)
+5…(10分)设t=
 ,则y=
,则y= t2-4t+5(t>0),…(11分)
t2-4t+5(t>0),…(11分)即y=
 (t-4)2-3.…(12分)
(t-4)2-3.…(12分)当t∈(0,4],即x∈[-2,+∞)时,y是t的减函数,t是x的减函数;…(13分)
当t∈[4,+∞),即x∈(-∞,-2]时,y是t的增函数,t是x的减函数;…(14分)
所以函数的单调递增区间是[-2,+∞),单调递减区间是(-∞,-2].…(16分)
分析:(Ⅰ)依题意,f(x)>5?
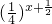 >
> ,利用指数函数的性质解之即可;
,利用指数函数的性质解之即可;(Ⅱ)令t=
 ,将f(x)=
,将f(x)=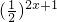 -
- +5转化为y=
+5转化为y= t2-4t+5(t>0),利用复合函数的单调性判断即可.
t2-4t+5(t>0),利用复合函数的单调性判断即可.点评:本题考查指数函数的单调性,考查函数单调性的判断与证明,考查转化思想与分类讨论思想的运用,考查复合函数的单调性,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)的图象是不间断的,有如下的x,f(x)对应值:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(x) | 136.136 | 15.552 | -3.92 | 10.88 | -52.488 | -232.064 | 11.238 |
由表可知函数f(x)存在实数解的区间有________个.
 .
. 的解集;
的解集; 的解集不是空集,求实数
的解集不是空集,求实数 的取值范围.
的取值范围.