题目内容
已知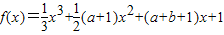 ,若方程f′(x)=0的两个实数根可以分别作为一个椭圆和双曲线的离心率,则( )
,若方程f′(x)=0的两个实数根可以分别作为一个椭圆和双曲线的离心率,则( )A.a-b<-3
B.a-b≤-3
C.a-b>-3
D.a-b≥-3
【答案】分析:f′(x)=x2+(a+1)x+(a+b+1),结合椭圆及双曲线的性质可得:f′(x)=x2+(a+1)x+(a+b+1)=0有一个大于1的根,一个小于1大于0,则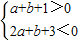 ,作出不等式组所表示的平面区域,利用线性规划的知识可求Z=a-b的范围
,作出不等式组所表示的平面区域,利用线性规划的知识可求Z=a-b的范围
解答:解:f′(x)=x2+(a+1)x+(a+b+1)
结合椭圆及双曲线的性质可得:f′(x)=x2+(a+1)x+(a+b+1)=0有一个大于1的根,一个小于1大于0作出不等式组
则
所表示的平面区域如图所示,令Z=a-b
作直线l:a-b=0,把直线向可行域平移到A(-2,1)时,Zmax=-3
∴a-b<-3
故选A.

点评:本题主要考查了函数的零点和根的分布,圆锥曲线的共同特征,线性规划的基础知识.考查基础知识的综合运用.
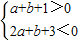 ,作出不等式组所表示的平面区域,利用线性规划的知识可求Z=a-b的范围
,作出不等式组所表示的平面区域,利用线性规划的知识可求Z=a-b的范围解答:解:f′(x)=x2+(a+1)x+(a+b+1)
结合椭圆及双曲线的性质可得:f′(x)=x2+(a+1)x+(a+b+1)=0有一个大于1的根,一个小于1大于0作出不等式组
则

所表示的平面区域如图所示,令Z=a-b
作直线l:a-b=0,把直线向可行域平移到A(-2,1)时,Zmax=-3
∴a-b<-3
故选A.

点评:本题主要考查了函数的零点和根的分布,圆锥曲线的共同特征,线性规划的基础知识.考查基础知识的综合运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
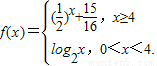 若方程f(x)-k=0有两个不等实根,则实数k的取值范围是 .
若方程f(x)-k=0有两个不等实根,则实数k的取值范围是 .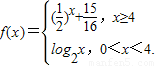 若方程f(x)-k=0有两个不等实根,则实数k的取值范围是 .
若方程f(x)-k=0有两个不等实根,则实数k的取值范围是 . 若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是 .
若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是 . ,若方程f′(x)=0的两个实数根可以分别作为一个椭圆和双曲线的离心率,则( )
,若方程f′(x)=0的两个实数根可以分别作为一个椭圆和双曲线的离心率,则( )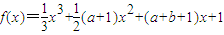 ,若方程f′(x)=0的两个实数根可以分别作为一个椭圆和双曲线的离心率,则( )
,若方程f′(x)=0的两个实数根可以分别作为一个椭圆和双曲线的离心率,则( )