题目内容
用
表示集合S中的元素的个数，设
为集合，称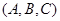
为有序三元组．如果集合满足
，且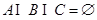
，则称有序三元组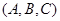为最小相交．由集合
的子集构成的所有有序三元组中，最小相交的有序三元组的个数为 ．
96
解析试题分析：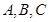
三个集合不可能有一元集，否则不能满足
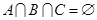，又因为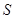
中只有4个元素，则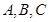中不可能有两个集合都有3个元素，否则不能满足，但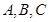中可以三个集合都含有2个元素，也可能是一个集合有3个元素，其它两个集合含有2个元素，情形如下：
如三个集合都含有2个元素这种情形
，
，
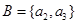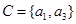，这种类型有
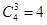种可能，另外第4个元素
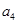可任意加入上述4种可能中的每一个集合，又形成不同的情形，这样就又有
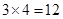种，于是就共有了
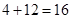种情形，在每一种情形
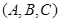中，它们的顺序可以打乱，每种可形成
个，因此共有
个有序三元组．
考点：集合的交集．
练习册系列答案
相关题目
有且只有一个元素，则a的值的集合(用列举法表示)是 .
是整数集
的非空子集，如果
有
，则称
关于数的乘法是封闭的. 若
,
是
且
有
有
，有四个命题：①
中至少有一个关于乘法是封闭的；②
，
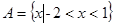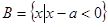，若
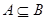，则实数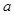
的取值范围是 ．
，集合
，则
．
，若
,求实数
的值为 ．
用列举法表示为 .
，
，
，求
；
，求实数a的取值范围．满足条件{1,2,3}
M{1,2,3,4,5,6}的集合M的个数是（ ）
| A．8 | B．7 | C．6 | D．5 |