题目内容
对于函数f(x)=x2+2x,在使f(x)≥M成立的所有常数M中,我们把M的最大值-1叫做f(x)=x2+2x的下确界. 则函数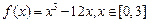 的下确界为
的下确界为
| A.0 | B.-27 | C.-16 | D.16 |
C
解析

练习册系列答案
相关题目
下列函数中,在区间(0,+∞)上是减函数的是 ( )
| A. y =" -" x2+2x | B. y =" x3" | C. y = 2-x+1 | D. y = log2x |
二次函数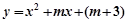 有两个不同的零点,着M取值范围为( )。
有两个不同的零点,着M取值范围为( )。
| A.(-2,6) | B.[-2,6] | C.{-2,6} | D.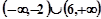 |
函数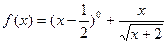 的定义域为( )
的定义域为( )
A.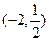 | B.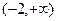 | C.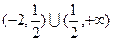 | D.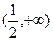 |
已知 ,且
,且 则
则 的值为
的值为
| A. 4 | B. 0 | C. 2m | D. |
设函数 是
是 上的奇函数,
上的奇函数,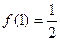 ,
,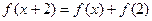 ,则
,则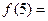 ( )
( )
| A.0 | B.1 | C.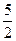 | D.5 |
若定义在R上的函数f(x)满足f(+x)=-f(x),且f(-x)=f(x),则f(x)可以是( )
| A.f(x)=2sinx | B.f(x)=2sin3x | C.f(x)=2cosx | D.f(x)=2cos3x |
函数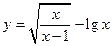 的定义域为( )
的定义域为( )
A.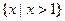 | B.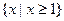 |
C.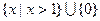 | D.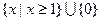 |
 是定义在
是定义在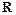 上的奇函数,当
上的奇函数,当 时,
时, .给出以下命题:
.给出以下命题: ①当
①当 时,
时, ; ②函数
; ②函数 的解集为
的解集为 ; ④
; ④ ,都有
,都有 .
.